Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì
△
A'B'C' đồng dạng
△
ABC nên 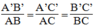
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB + 10,8cm = 16,2 + 10,8 = 27 (cm)
Ta có: 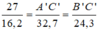
Suy ra: 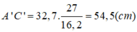
Suy ra: 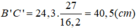

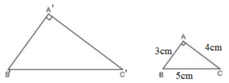
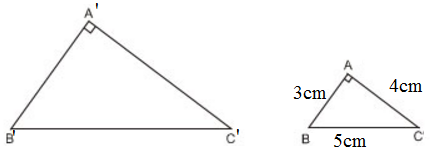
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
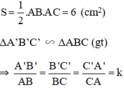
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
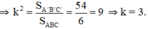
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.

Vì
△
A'B'C' đồng dạng
△
ABC nên 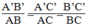
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB - 5,4 = 16,2 - 5,4 =10,8 (cm)
Ta có: 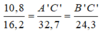
Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)
B'C'= (10,8 . 24,3): 16,2 = 16,2 (cm)

Có độ dài của các cạnh tam giác ABC rồi mà đáng lẽ phải tính các cạnh của tam giác A'B'C' chứ ????
Tự vẽ hình nha :"))))
Ta có tam giác ABC đồng dạng với tam giác A'B'C'
\(\Rightarrow\frac{S_{ABC}}{S_{A'B'C'}}=\left(\frac{AB}{A'B'}\right)^2\)
Mà tam giác ABC có độ dài các cạnh là 3,4,5 nên là tam giác vuông
\(\Rightarrow S_{ABC}=\frac{1}{2}.3.4=6\left(cm^2\right)\)
\(\Rightarrow\frac{6}{54}=\left(\frac{AB}{A'B'}\right)^2\Rightarrow\left(\frac{AB}{A'B'}\right)^2=\frac{1}{9}\Rightarrow\frac{AB}{A'B'}=\frac{1}{3}\)
\(\Rightarrow A'B'=3.AB=3.3\)
Nên mỗi cạnh của tam giác A'B'C' gấp 3 lần của cạnh của tam giác ABC.
Suy ra ba cạnh của tam giác A'B'C là 9cm, 12cm, 15cm
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng
\(S=\frac{1}{2}.AB.AC=6\left(cm^2\right)\)
\(\Delta ABC~\Delta A'B'C'\left(gt\right)\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k\)
( với k là tỉ số đồng dạng ).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
\(\Rightarrow k^2=\frac{S_{A'B'C'}}{S_{ABC}}=\frac{54}{6}=9\Rightarrow k=3\)
\(\Rightarrow A'B'=3.AB=3.3=9\left(cm\right)\)
\(B'C'=3.BC=3.5=15\left(cm\right)\)
\(C'A'=3.CA=3.4=12\left(cm\right)\)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)