
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\Leftrightarrow\left\{{}\begin{matrix}6x=-12\\x-2y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\2y=x+8=-2+8=6\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(-2;3\right)\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}x-2y=5\\x-2y=5\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}3x-3y=9\\3x-3y=1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}-5y=5\\3x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=0\end{matrix}\right.\)

\(=\dfrac{x+6\sqrt{x}+5+x-5\sqrt{x}-x+9\sqrt{x}+20}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{x+10\sqrt{x}+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{\left(\sqrt{x}+5\right)^2}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{\sqrt{x}+5}{\sqrt{x}-5}\)

a: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Ta có: \(\widehat{KOA}+\widehat{BOA}=\widehat{KOB}=90^0\)
\(\widehat{KAO}+\widehat{COA}=90^0\)(ΔOCA vuông tại C)
mà \(\widehat{BOA}=\widehat{COA}\)
nên \(\widehat{KOA}=\widehat{KAO}\)
=>KA=KO
d: Xét (O) có
\(\widehat{ACI}\) là góc tạo bởi tiếp tuyến CA và dây cung CI
\(\widehat{CDI}\) là góc nội tiếp chắn cung CI
Do đó: \(\widehat{ACI}=\widehat{CDI}\)
ΔOCA vuông tại C
=>\(CO^2+CA^2=OA^2\)
=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Xét ΔACI và ΔADC có
\(\widehat{ACI}=\widehat{ADC}\)
\(\widehat{CAI}\) chung
Do đó: ΔACI đồng dạng với ΔADC
=>\(\dfrac{AC}{AI}=\dfrac{AD}{AC}\)
=>\(AI\cdot AD=AC^2=\left(R\sqrt{3}\right)^2=3R^2\) không đổi

Xét tg ABO và tg ACO có
AO chung
AB=AC (gt)
OB=OC=R
=> tg ABO = tg ACO (c.c.c)
\(\Rightarrow\widehat{ACO}=\widehat{ABO}=90^o\Rightarrow AC\perp OC\) => AC là tiếp tuyến với (O)
b/
Xét tg vuông EOI và tg vuông COI có
OE=OC=R; OI chung => tg EOI = tg COI (hai tg vuông có 2 cạnh góc vuông bằng nhau)
Xét tg vuông EDI và tg vuông CDI có
DI chung
tg EOI = tg COI (cmt) => IE=IC
=> tg EDI = tg CDI (hai tg vuông có 2 cạnh góc vuông bằng nhau)
Xét tg DEO và tg DCO có
DO chung
OE=OC=R
tg EDI = tg CDI (cmt) => DE=DC
=> tg DEO = tg DCO (c.c.c)
\(\Rightarrow\widehat{DEO}=\widehat{DCO}=90^o\Rightarrow DE\perp OE\) => DE là tiếp tuyến với (O, R)


b: Xét ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC
nên \(AH^2=AC\cdot AK\)
\(\Leftrightarrow\dfrac{AC}{2}=\dfrac{AH^2}{2\cdot AK}\)
hay \(HI=\dfrac{AH^2}{2\cdot AK}\)

Bài 2:
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2m-n+1=3\\4m-n+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m+n=-2\\4m-n=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6m=-4\\4m-n=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{2}{3}\\n=4m+2=-\dfrac{8}{3}+2=-\dfrac{2}{3}\end{matrix}\right.\)

Hướng dẫn:
Ta có:
\(x^2-xy+y^2=2x-3y-2\)
\(\Leftrightarrow2x^2-2xy+2y^2-4x+6y+4+9=9\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2+6y+9\right)=9\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y+3\right)^2=9\)
Xét....
Đây là 1 cách nhưng làm hơi dài.
\(x^2-xy+y^2=2x-3y-2\\ \Leftrightarrow x^2-xy+y^2-2x+3y+2=0\left(1\right)\\ \Leftrightarrow x^2-x\left(y+2\right)+y^2+3y+2=0\)
Coi đây là pt bậc 2 ẩn x
Ta có: \(\Delta=\left[-\left(y+2\right)\right]^2-4\left(y^2+3y+2\right)=y^2+4y+4-4y^2-12y-8=-3y^2-8y-4\)
Để pt có nghiệm nguyên thì \(\Delta\ge0\Leftrightarrow-3y^2-8y-4\ge0\Leftrightarrow-2\le y\le-\dfrac{2}{3}\)
\(\Leftrightarrow y\in\left\{-2;-1\right\}\)
Thay y=-2 vào (1) ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-2\right)+\left(-2\right)^2-2x+3.\left(-2\right)+2=0\\ \Leftrightarrow x^2+2x+4-2x-6+2=0\\ \Leftrightarrow x^2=0\Leftrightarrow x=0\)
Thay y=-1 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-1\right)+\left(-1\right)^2-2x+3.\left(-1\right)+2=0\\ \Leftrightarrow x^2+x+1-2x-3+2=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-2\right);\left(0;-1\right);\left(1;-1\right)\right\}\)


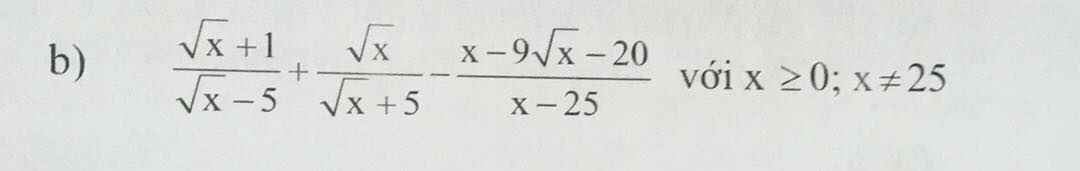
 giải giúp mình với ạa , mình cảm ơn.
giải giúp mình với ạa , mình cảm ơn.
 Giúp mình giải với mng ơi chiều mình cần gấppp
Giúp mình giải với mng ơi chiều mình cần gấppp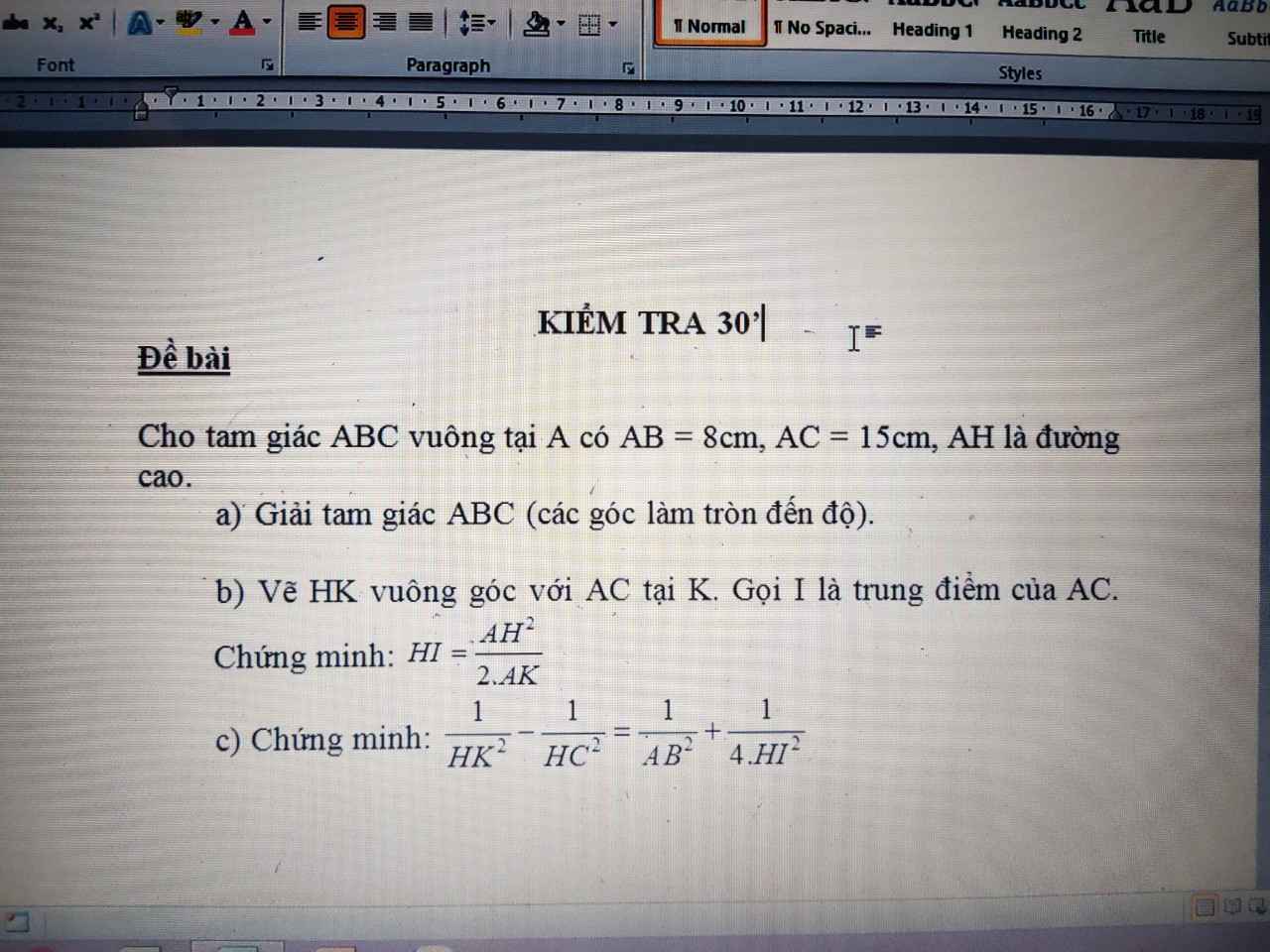


Cậu có thể giải hộ mình được không?