K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
24 tháng 9 2021
Lời giải:
$b=2021^0=1< 26^9=a$
$c=26^9=(2.13)^9=2^9.13^9=(2^3)^3.13^9=8^3.13^9<13^3.13^9$
$=13^{12}< 13^{15}=a$
Vậy $b< c< a$
Đáp án C.
H9
HT.Phong (9A5)
CTVHS
10 tháng 8 2023
Bài 13:
Ta có: a // b
\(\Rightarrow\widehat{G}=x=\left(180^o-138^o\right)+42^o=84^o\)
Bài 14:
Ta có: \(Cz\perp CB\) và \(By\perp CB\)
\(\Rightarrow Cz//By\)
Ta có:
\(\widehat{ABC}=\left(180^o-90^o\right)+\left(180^o-140^o\right)=90^o+40^o=130^o\) (đúng)
\(\Rightarrow Ax//By\)
10 tháng 8 2023
14:
By vuông góc BC
BC vuông góc Cz
=>By//Cz
Gọi Bm là tia đối của tia By
=>góc mBC=90 độ
góc mBA=130-90=40 độ
góc mBA+góc BAx=180 độ
mà hai góc này trong cùng phía
nên Bm//Ax
=>By//Ax//Cz
XO
1 tháng 11 2019
Ta có : xy + x + y = 30
=> (xy + x) + y = 30
=> x(y + 1) + (y+ 1) = 31
=> (x + 1)(y + 1) = 31
Lại có 31 = 1.31 = 31.1
Lập bảng xét 2 trường hợp ta có :
| x + 1 | 1 | 31 |
| y + 1 | 31 | 1 |
| x | 0 | 30 |
| y | 30 | 0 |
Vậy các cặp số (x;y) thỏa mãn là : (30 ; 0) ; (0 ; 30)
M
1 tháng 11 2019
Bài giải
\(xy+x+y=30\)
\(x\left(y+1\right)+y=30\)
\(x\left(y+1\right)+\left(y+1\right)=30+1\)
\(x\left(y+1\right)+\left(y+1\right)=31\)
\(\left(x+1\right)\left(y+1\right)=31\)
\(\Rightarrow\text{ }x+1\text{ , }y+1\inƯ\left(31\right)\)
Ta có bảng :
| x + 1 | - 1 | 1 | - 31 | 31 |
| y + 1 | - 31 | 31 | - 1 | 1 |
| x | - 2 | 0 | - 32 | 30 |
| y | - 32 | 30 | - 2 | 0 |
\(\text{Vậy các cặp }\left(x,y\right)=\left(-2\text{ ; }32\right),\left(0\text{ ; }30\right),\left(-32\text{ ; }-2\right),\left(30\text{ ; }0\right)\)
VB
3
2
21 tháng 4 2021
a. ( x - 2 ) ( 6 - 2x ) = 0
=> x - 2 = 0 hoặc 6 - 2x = 0
x = 2 2x = 6
x = 3
Vậy x = 2; x =3
b. ( x + 1 )3 = -27
( x + 1 )3 = ( -3 )3
=> x + 1 = -3
x = -4
10 tháng 8 2023
a: =4*1/16+25*[(3/4:5/4)]^3:27/8
=1/4+25*(3/5:3/2)^3
=1/4+25*(2/5)^3
=1/4+8/5
=1,6+0,25=1,85
b: =8+3-1+8-8
=8+2=10
25 tháng 12 2020
XY+14+2y+7x=-10
xy*xy+14+2+7=-10
xy*xy+23=-10
xy2=-10-23
xy2=-33
VD
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 12 2022
nếu p = 2 ta có : p + 2 = 2 + 2 = 4 (loại)
nếu p > 2 vì p là số nguyên tố mà p> 2 nên p là số lẻ => p = 2k + 1 (k\(\ge\)1)
=> p + 1 = 2k + 1 + 1 = 2k + 2 = 2.(k+1) (loại)
vậy không có giá trị nào của p thỏa mãn đề bài
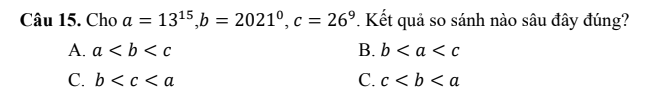
Lời giải:
Gọi số hs khối 6 là $a$. Khi xếp hàng 12, 15, 18 thừa $5$ hs nên $a-5$ chia hết cho $12,15,18$
$\Rightarrow a-5\vdots \text{BCNN(12,15,18)}$
Dễ thấy $\text{BCNN(12,15,18)}=180$
$\Rightarrow a-5\vdots 180$
$\Rightarrow a-5\in\left\{180; 360; 540; ...\right\}$
$\Rightarrow a\in\left\{185; 365; 545;...\right\}$
Mà $a$ trong khoảng từ $200$ đến $400$ nên $a=365$ (hs)
thanks bn