Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Động năng bằng thế năng ở vị trí x = ±A√2/2 = ±√2 cm và v = ωA/√2 = 6π cm.
+ Khi mo rơi và dính vào m, theo định luật bảo toàn động lượng (chú ý là vật m0 rơi thẳng đứng nên động lượng của nó theo phương ngang = 0): (m+mo)v’ = mv => v’ = 4π cm/s.
+ Hệ (m + mo) có ω’ = 2π√3 rad/s và qua VTCB vận tốc của hệ là:
![]()
![]()
![]()

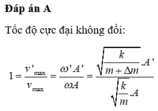
- Áp dụng định luật bảo toàn động lượng, ta có
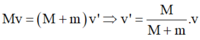
(với v và v’ là vận tốc cực đại của hệ lúc đầu và lúc sau)
- Ban đầu, cơ năng của hệ:
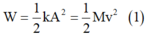
Lúc sau, cơ năng của hệ:
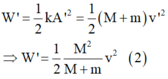
- Lập tỉ số (2) và (1) ta thu được kết quả:
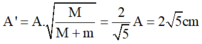

Đáp án A
+ Áp dụng định luật bảo toàn động lượng, ta có:
Mv = (M+m) v ' ⇒ v ' = M M + m . v (với v và v’ là vận tốc cực đại của hệ lúc đầu và lúc sau)
+ Ban đầu, cơ năng của hệ: W = 1 2 k A 2 = 1 2 M . v 2 (1)
+ Lúc sau, cơ năng của hệ:

+ Lập tỉ số (2) và (1) ta thu được kết quả: A ' = A . M M + m = 2 5 A = 2 5 c m
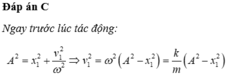
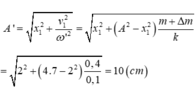

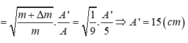





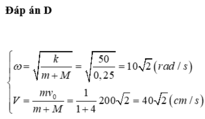
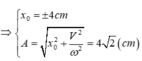
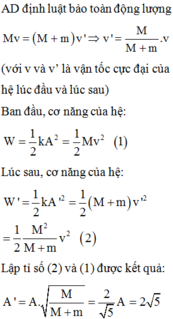
Mình cũng không hiểu đề lắm :)
Mà các bài toán về va chạm không thi đâu bạn ơi, không nên học.
Không chắc lắm:
+) TH1 v1\(\uparrow\downarrow\)v2 => A=2cm ( vận tốc tại biên = 0)
+) TH2 v1\(\uparrow\uparrow v2\) => \(v=\frac{m1.v1+m2.v2}{m1+m2}=v1\Rightarrow\)cơ năng vật ( m1+m2) sau va chạm 1/2(m1+m2).V^2=1/2.k.A^2 suy ra A=2A0