
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)


a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC

Xảy ra khi điều kiện đặt ra so với biến luôn đúng nên câu lệnh sẽ luôn được thực hiện
Khắc phục:thay đổi điều kiện hoặc gán lại giá trị cho biến để cho biến đủ nhỏ hoặc l

a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4
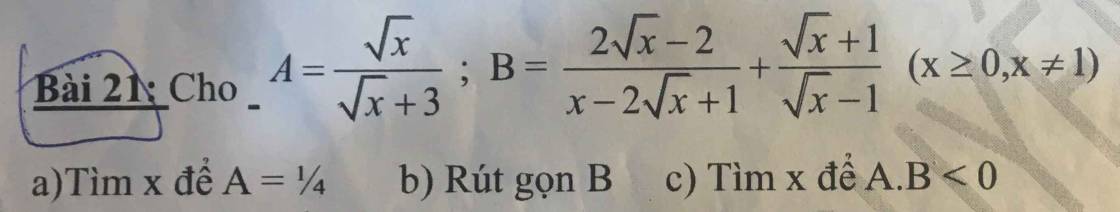

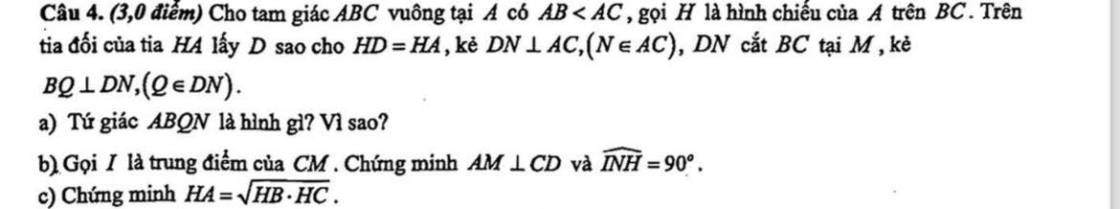

 mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
a, đkxđ: \(x\ge0\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}=\dfrac{1}{4}\Leftrightarrow\sqrt{x}+3=4\sqrt{x}\Leftrightarrow3=3\sqrt{x}\Leftrightarrow\sqrt{x}=1\Leftrightarrow\left(\sqrt{x}\right)^2=1^2\Leftrightarrow x=1\)
b,
\(B=\dfrac{2\sqrt{x}-2}{x-2\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{2\sqrt{x}-2+x-1}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}+1\right)^2-4}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\)
c,
\(A.B< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+3}.\dfrac{\sqrt{x}+3}{\sqrt{x}-1}< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}< 0\)
do \(\sqrt{x}\ge0\) mà \(\frac{\sqrt{x}}{\sqrt{x}-1}<0\Leftrightarrow \sqrt{x}-1<0\Leftrightarrow \sqrt{x}<1\Leftrightarrow x<1\)