
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(=\left(1-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\right):\left(\dfrac{-\left(\sqrt{x}-3\right)}{\sqrt{x}-2}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}+\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\dfrac{\sqrt{x}+3-\sqrt{x}+3}{\sqrt{x}+3}:\dfrac{-x+9+x-4\sqrt{x}+4+x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{6}{\sqrt{x}+3}\cdot\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{x-4\sqrt{x}+4}=\dfrac{6}{\sqrt{x}-2}\)
b: Để A nguyên thì \(\sqrt{x}-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(x\in\left\{1;16;0;25;64\right\}\)
\(1-\dfrac{x-3\sqrt{x}}{x-9}=1-\dfrac{\sqrt{x}}{\sqrt{x}+3}\) chứ nhỉ?

B=\(\left(\dfrac{a+\sqrt{a}}{\sqrt{a}+1}+1\right)\)+\(\left(\dfrac{a-\sqrt{a}}{\sqrt{a}-1}+1\right)\left(x\ge0,x\ne1\right)\)
\(B=\)\(\left[\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}+1\right]+\left[\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}+1\right]\)
\(B=\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)=2\sqrt{a}+2\)
b, ĐỂ B=\(\sqrt{a}+1< =>2\sqrt{a}+2=\sqrt{a}+1\)
<=>\(\sqrt{a}=-1\)(vô lí)
vậy a\(\in\phi\)

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

\(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\Rightarrow C=\dfrac{x+3}{\sqrt{x}}=\sqrt{x}+\dfrac{3}{\sqrt{x}}\ge2\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}}}=2\sqrt{3}\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{3}{\sqrt{x}}\Rightarrow x=3\)

`a,` ĐKXĐ: `x>=0;x\ne1`
`A=...=(sqrtx(1+sqrtx)+sqrtx(1-sqrtx)+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(sqrtx+x+sqrtx-x+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(3sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=-3/(1+sqrtx)`
`b,A=-3/(1+sqrtx)`
Vì `x>=0` nên `1+sqrtx>=1` nên `3/(1+sqrtx)<=3` suy ra `A>=-3`
Dấu "=" xảy ra `<=>x=0`
Vậy `A_(min)=-3<=>x=0`







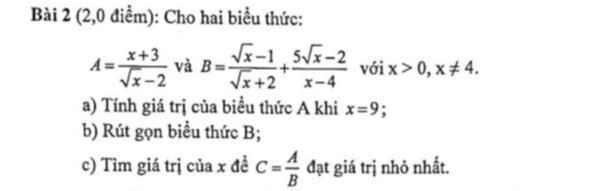 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ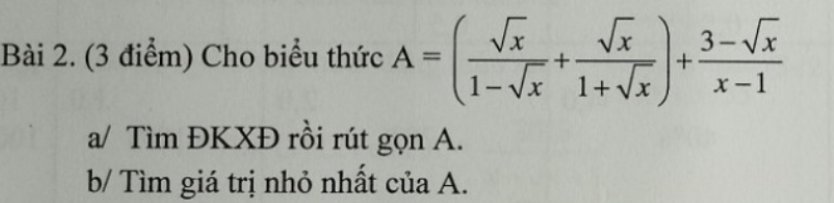
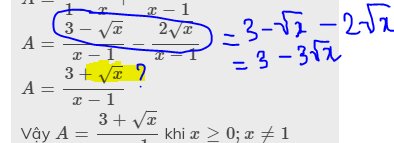


Câu 6
a: Xét (O) có
DB,DC là tiếp tuyến
nên DB=DC
=>ΔDBC cân tại D
b: Xét (O) cos
ΔCABnội tiếp
AB là đường kính
=>ΔCAB vuông tại C
OB=OC
DB=DC
=>ODlà trung trực của BC
=>OD vuông góc với BC
mà AC vuông góc BC
nên OD//AC
d: Xét ΔCAB vuông tại C có
cos CAO=CA/CB=1/2
=>góc CAO=60 độ
=>ΔOAC đều
=>góc BOC=120 độ
=>góc BDC=60 độ
mà ΔBDC cân tại D
nên ΔBCD đều
\(CB=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(S_{BCD}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\sqrt{3}\cdot R^2}{4}\)