K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
11 tháng 12 2021
\(b,x,y\) TLN \(\Rightarrow x.y=a_1\Rightarrow x=\dfrac{a_1}{y}\)
\(y,x\) TLT \(\Rightarrow y=a_2z\)
\(\Rightarrow x=\dfrac{a_1}{a_2z}=\dfrac{\dfrac{a_1}{a_2}}{z}\Rightarrow x=\dfrac{k}{z}\)
Do đó x TLN với z
22 tháng 10 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}=\dfrac{a+b+c+d}{2+3+4+5}=\dfrac{140}{14}=10\)
Do đó: a=20; b=30; c=40; d=50
2 tháng 7 2023
3:
\(A=\dfrac{-1}{3}x^2y+\dfrac{2}{5}x^3-8xy-\dfrac{2}{3}x^2y-\dfrac{2}{5}x^3+xy-4-1\)
=-x^2y+7xy-5
Khi x=-1/3 và y=2 thì A=-1/9*2+7*(-1/3)*2-5
=-2/9-14/3-5
=-2/9-42/9-45/9
=-89/9
9 tháng 2 2022
Dấu hiệu là số lượng hsinh nữ trong 1 trường THCS
Có 30GT
| GT(x) | 6 | 12 | 14 | 16 | 18 | 17 | 19 | 20 | 13 | 10 15 25 |
| Tần số (n) | 1 | 2 | 3 | 5 | 3 | 4 | 3 | 3 | 1 | 1 3 1. N= 30 |
Có 12 GT khác nhau
Giá trị có tần số lớn(nhỏ) nhất là 16(6;13;10;25)
Mốt của dấu hiệu 14 --> 17
DH
9 tháng 2 2022
a) dấu hiệu cần tìm là : số lượng học sinh nữ của mỗi lớp
- Dấu hiệu đó có tất cả 30 giá trị
b) bảng tần số giờ ko lập dc ở đây
TA
1
18 tháng 11 2023
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOMA=ΔOMB
b: ΔOMA=ΔOMB
=>MA=MB và OA=OB
OA=OB
=>O nằm trên đường trung trực của AB(1)
MA=MB
=>M nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB
S
2
25 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }x+y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/3 = (x+y)/(2 + 3) = 50/5 = 10`
`=> x/2 = y/3 = 10`
`=> x = 10*2 = 20; y = 3*10 = 30`
Vậy, `x = 20; y = 30`
`b)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }5x+4y=110\)
Ta có:
`x/2 = y/3` `=> (5x)/10 = (4y)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(5x)/10 = (4y)/12 = (5x+4y)/(10 + 12) = 110/22 = 5`
`=> x/2 = y/3 = 5`
`=> x = 2*5 = 10; y = 3*5 = 15`
Vậy, `x = 10; y = 15`
`c)`
\(5x=11y\text{ và }2x+3y=37\)
Ta có:
`5x = 11y -> x/11 = y/5 -> (2x)/22 = (3y)/15`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/22 = (3y)/15 = (2x+3y)/(22+15) = 37/37 = 1`
`=> x/11 = y/5 = 1`
`=> x = 11; y = 5`
Vậy, `x = 11; y = 5`
`d)`
\(\dfrac{x}{2}=\dfrac{y}{1}\text{và }x+y-63=0\)
Ta có: `x + y - 63 = 0 -> x + y = 63`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/1 = (x+y)/(2+1) = 63/3 = 21`
`=> x/2 = y/1 = 21`
`=> x = 21*2 =42; y = 21`
Vậy, `x = 42; y = 21.`
NN
25 tháng 7 2023
`2,`
`a)`
\(\dfrac{a}{14}=\dfrac{b}{2}=\dfrac{c}{4}\text{ và }a+b+c=5\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`a/14 = b/2 = c/4 = (a+b+c)/(14+2+4)=5/20=1/4=0,25`
`=> a/14 = b/2 = c/4 = 0,25`
`=> a = 14*0,25 = 3,5` `; b = 2*0,25 = 0,5;` `c = 4*0,25 = 1`
Vậy, `a = 3,5`; `b = 0,5`; `c = 1`
`b)`
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\text{ và }7a+3b-5c=7\)
Ta có:
`a/3 = b/5 = c/8 => (7a)/21 = (3b)/15 = (5c)/40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(7a)/21 = (3b)/15 = (5c)/40 = (7a + 3b - 5c)/(21 + 15 - 40)=7/-4 = -1,75`
`=> a/3 = b/5 = c/8 = -1,75`
`=> a = 3*(-1,75) = -5,25`
`b = 5*(-1,75) = -8,75`
`c = 8*(-1,75) = -14`
Vậy, `a = -5,25; b = -8,75`; `c = -14`
`c)`
\(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\text{và }3a+b-2c=14\)
Ta có:
`a/3 = b/8 = c/5 -> (3a)/9 = b/8 = (2c)/10`
Câu này bạn làm tương tự nha
`d)`
\(\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\text{ và }3a+5c-7b=30\)
Ta có:
`a/3 = b/2 -> a/21 = b/14`/
`b/7 = c/5 -> b/14 = c/10`
`=> a/21 = b/14 = c/10`
`=> (3a)/63 = (7b)/98 = (5c)/50`
Câu này bạn cũng làm tương tự.
21 tháng 12 2020
Bài 4:
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
b) Ta có: ΔABD=ΔAED(cmt)
nên \(\widehat{ABD}=\widehat{AED}\)(hai góc tương ứng)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)(cmt)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: ΔABD=ΔAED(cmt)
nên BD=ED(hai cạnh tương ứng)
Xét ΔBDF và ΔEDC có
BD=ED(cmt)
\(\widehat{FBD}=\widehat{CED}\)(cmt)
BF=EC(gt)
Do đó: ΔBDF=ΔEDC(c-g-c)
⇒DF=DC(hai cạnh tương ứng)
c) Ta có: ΔBDF=ΔEDC(cmt)
nên \(\widehat{BDF}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{BDF}+\widehat{CDF}=180^0\)(hai góc kề bù)
nên \(\widehat{EDC}+\widehat{FDC}=180^0\)
\(\Leftrightarrow\widehat{EDF}=180^0\)
hay E,D,F thẳng hàng(đpcm)
d) Ta có: AB+BF=AF(B nằm giữa A và F)
AE+EC=AC(E nằm giữa A và C)
mà AB=AE(gt)
và BF=EC(gt)
nên AF=AC
hay A nằm trên đường trung trực của CF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DF=DC(cmt)
nên D nằm trên đường trung trực của CF(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
hay AD⊥FC(đpcm)
??????????????????????
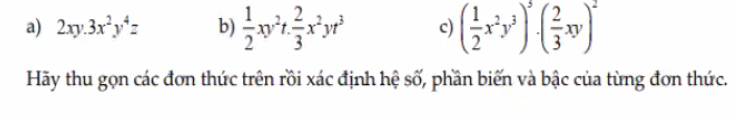
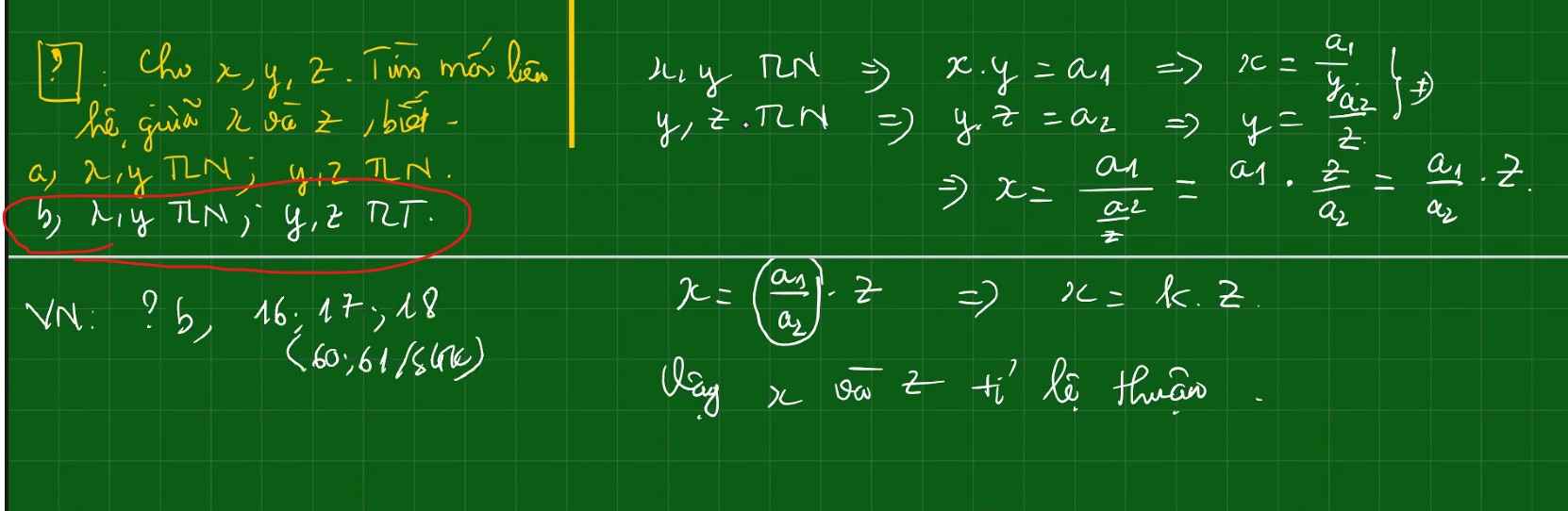
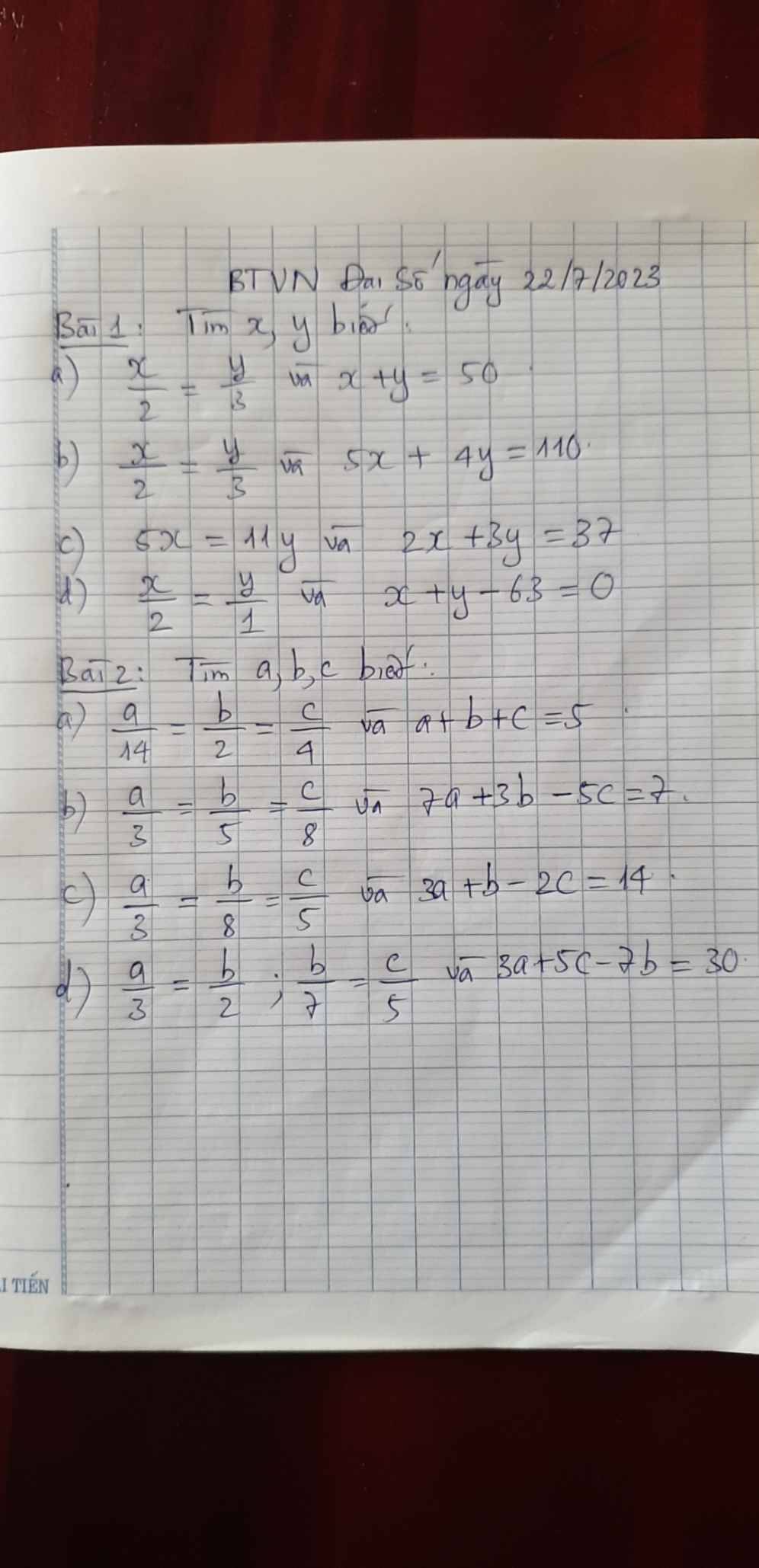
Đâu vậy?