
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: A=x^2+4x+4+5
=(x+2)^2+5>=5
Dấu = xảy ra khi x=-2
b: =3/2(x^2+2/3x+2/3)
=3/2(x^2+2*x*1/3+1/9+5/9)
=3/2(x+1/3)^2+15/18>=15/18=5/6
Dấu = xảy ra khi x=-1/3
e: =x^2-2x+1+4
=(x-1)^2+4>=4
Dấu = xảy ra khi x=1
f: =2(x^2-3x)
=2(x^2-3x+9/4-9/4)
=2(x-3/2)^2-9/2>=-9/2
Dấu = xảy ra khi x=3/2
h: =-(x^2-4x-3)
=-(x^2-4x+4-7)
=-(x-2)^2+7<=7
Dấu = xảy ra khi x=2


a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC

bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu

a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4

a: ĐKXĐ: x<>0; x<>1(A)
(B): x<>0; x<>3
(C): x<>2; x<>-2
b: \(A=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(B=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(C=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
c: Khi x=0 thì A và B không xác định
Khi x=0 thì C=3/2
Khi x=3 thì B ko xác định, A=2/3; C=3/5
\(a,DKXD:\)
\(+x^2-x\ne0\Leftrightarrow x\ne0;1\)
\(+x^2-3x\ne0\Leftrightarrow x\ne0;3\)
+\(x^2-4\ne0\Leftrightarrow x\ne\pm4\)
\(b,\)
\(\dfrac{2x-2}{x^2-x}=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(\dfrac{2x-6}{x^2-3x}=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(\dfrac{3x-6}{x^2-4}=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
\(c,\)
Vì phân thức 1,2 cùng kết quả nên mk lm 1 cái thôi nhé
+ Thay \(x=0\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{0}=0\)
Thay \(x=3\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{3}\)
+ Thay \(x=0\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{0+2}=\dfrac{3}{2}\)
Thay \(x=3\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{3+2}=\dfrac{3}{5}\)
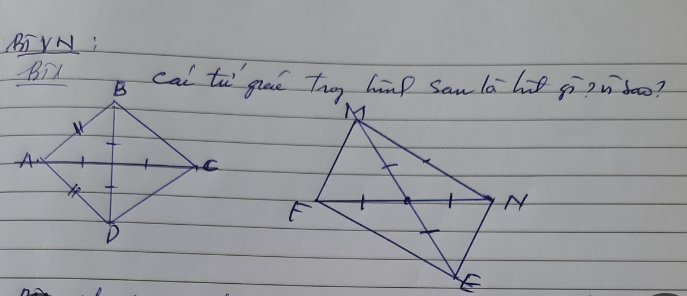
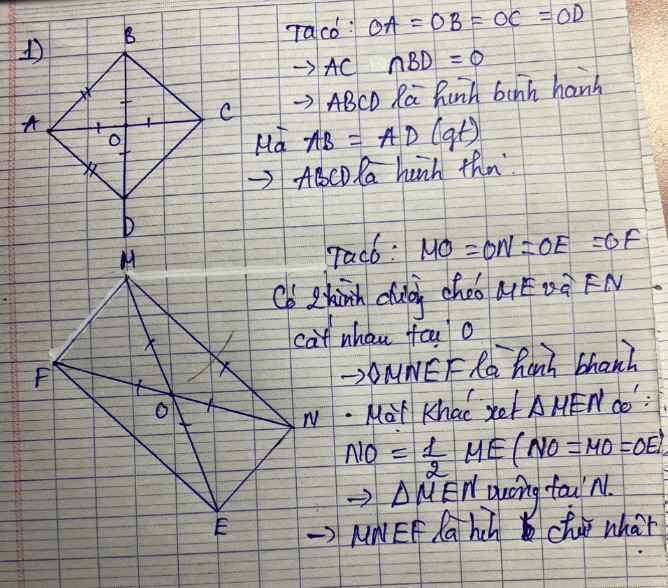
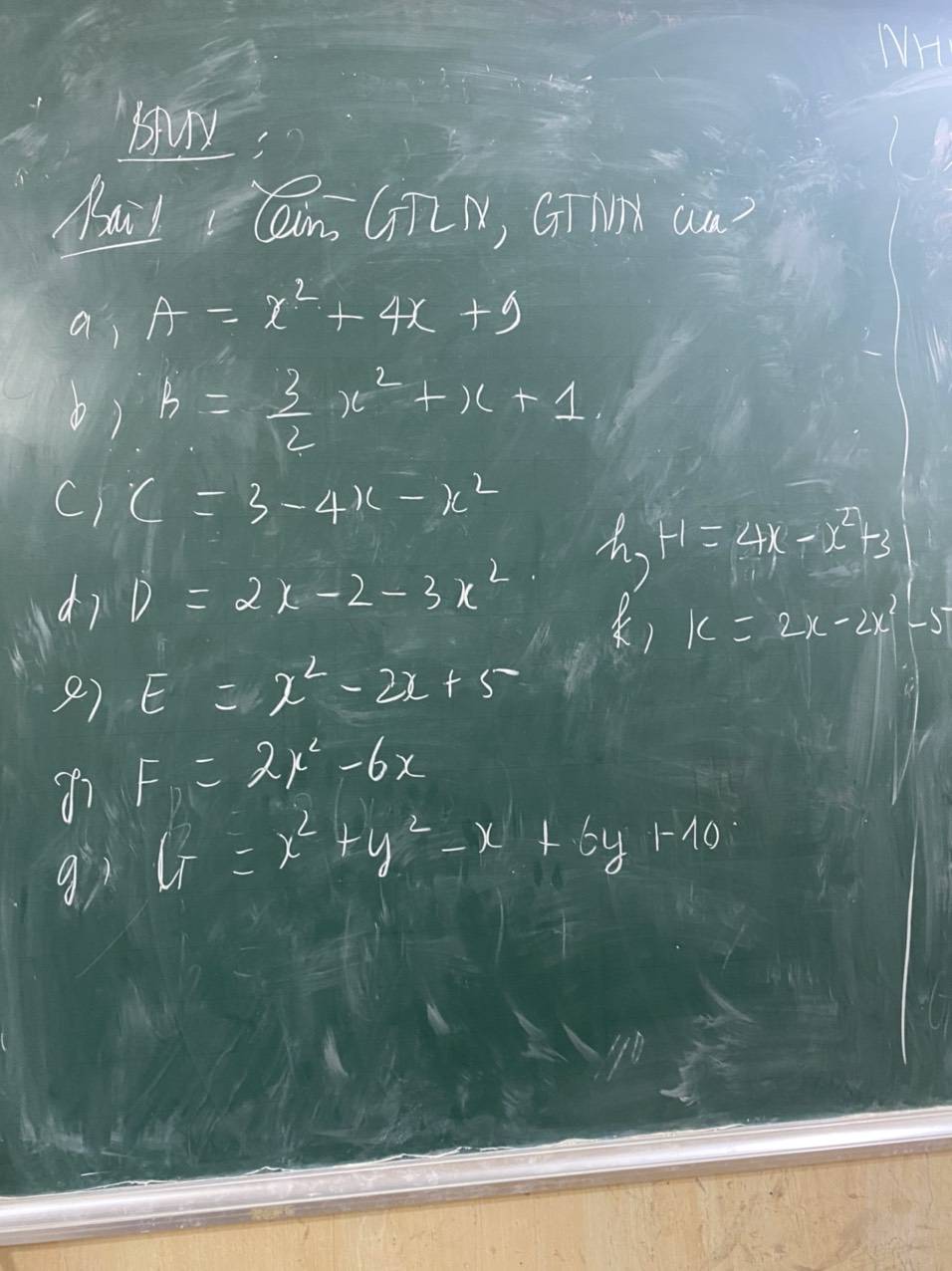


 mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
a, Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{x}=\dfrac{5}{10}\Rightarrow x=4:\dfrac{1}{2}\Rightarrow x=8\)
Áp dụng hệ quả định lý Ta-lét ta có:
\(\dfrac{AE}{AC}=\dfrac{DE}{BC}\Rightarrow\dfrac{5}{15}=\dfrac{6}{y}\Rightarrow y=6:\dfrac{1}{3}\Rightarrow y=18\)
b, Áp dụng định lý phân giác ta có:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\Rightarrow\dfrac{5}{6}=\dfrac{10}{x}\Rightarrow x=10:\dfrac{5}{6}\Rightarrow x=12\)