
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý

ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển

\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)

1, \(\sqrt{\frac{-12}{x-5}}\) xác định khi \(\frac{-12}{x-5}\) \(\ge\) 0
→x-5<0→x<5
3. xác định khi x-2>0 →x>2
5.xác định khi \(\frac{4x-5}{x+2}\ge0\)và x\(\ne\)-2
→\(\left[\begin{array}{nghiempt}\hept{\begin{cases}4x-5< 0\\x-3< 0\end{array}\right.\\\hept{\begin{cases}4x-5\ge0\\x-3>0\end{array}\right.\end{cases}\Rightarrow\left[\begin{array}{nghiempt}\hept{\begin{cases}x< \frac{5}{4}\\x< 3\end{array}\right.\\\hept{\begin{cases}x\ge\frac{5}{4}\\x>3\end{array}\right.\end{array}\right.}\)







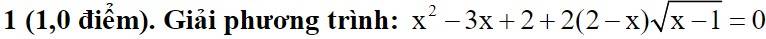
 Anh chị giúp e 1 tay với ạ ? Em cảm ơn nhiều
Anh chị giúp e 1 tay với ạ ? Em cảm ơn nhiều
\(VT=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{35}}}.\left(3\sqrt{2}+\sqrt{14}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{5}.\sqrt{7}}}.\left(3\sqrt{2}+\sqrt{2}.\sqrt{7}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{\sqrt{5}\left(8+3\sqrt{7}\right)}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\sqrt{\dfrac{1}{8+3\sqrt{7}}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\dfrac{\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{8+3\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}.\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{2}.\sqrt{8+3\sqrt{7}}}\) (Nhân \(\sqrt{2}\) cả tử và mẫu)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{16+6\sqrt{7}}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{\left(3+\sqrt{7}\right)^2}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\left|3+\sqrt{7}\right|}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{3+\sqrt{7}}\)
\(=2=VP\left(dpcm\right)\)
e cảm mơn ạ