K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2
13 tháng 1 2023
Số cách lấy ra `5` quả bất kì là: `C_10 ^5=252` cách
Số cách lấy ra `5` quả nhưng trong đó không có quả cầu xanh: `C_6 ^5=6` cách
`=>` Số cách lấy ra `5` quả bất kì trong đó có ít nhất `1` cầu xanh là: `252-6=246` cách
(Tối đa có `252` cách lấy mà bạn lại tính ra `504` là điều vô lí, với bài này dùng đối của yêu cầu đề bài sẽ thích hợp nhất)
DT
3 tháng 5 2022
18C
22D
26B
Giải thích thêm:
ta có: v=s'(t)=3t²-6t+6
a=s"(t)=6t-6
Thời điểm gia tốc bị triệt tiêu khi a=0
⇔6t-6=0
⇔t=1
Vậy v=3.1²-6.1+6=3 (m/s)
32A
34C
35A
NL
3 tháng 5 2022
cho mình hỏi là tại sao ở câu 26 lại phải đạo hàm thêm lần nữa vậy?
PN
0
HP
13 tháng 8 2021
a, \(sin^2x+sinx.cosx=\dfrac{1}{2}\)
\(\Leftrightarrow2sin^2x-1+2sinx.cosx=0\)
\(\Leftrightarrow sin2x-cos2x=0\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow2x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
Do chóp tứ giác đều \(\Rightarrow\Delta SAC\) cân tại A
Mà O là tâm đáy \(\Rightarrow O\) là trung điểm AC
\(\Rightarrow SO\perp AC\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Hoàn toàn tương tự, ta có \(SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)
b.
Ta có: \(AC\perp BD\) (hai đường chéo hình vuông)
Theo cmt, \(SO\perp AC\)
\(\left\{{}\begin{matrix}SO\in\left(SBD\right)\\BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Tương tự: \(\left\{{}\begin{matrix}BD\perp AC\\BD\perp SO\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
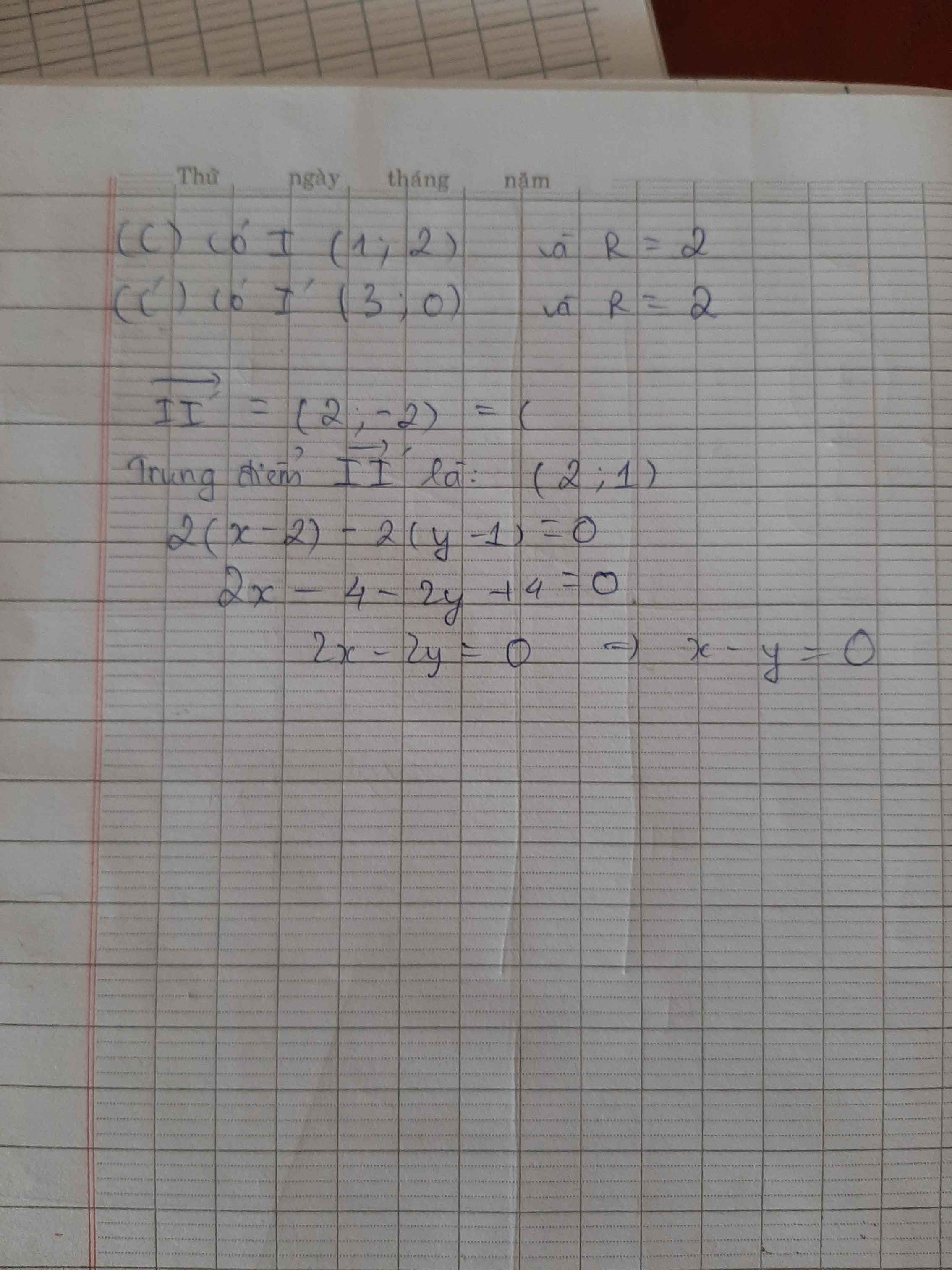
Coi lại giúp với