
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ký hiệu S,p lần lượt là diện tích và nửa chu vi của tam giác ABC.
\(r=r_a-r_b-r_c\)
\(\Leftrightarrow\dfrac{S}{p}=\dfrac{S}{p-a}-\dfrac{S}{p-b}-\dfrac{S}{p-c}\)
\(\Leftrightarrow\dfrac{1}{a+b+c}=\dfrac{1}{b+c-a}-\dfrac{1}{c+a-b}-\dfrac{1}{a+b-c}\)
\(\Leftrightarrow\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}=\dfrac{1}{b+c-a}-\dfrac{1}{a+b+c}\)
\(\Leftrightarrow\dfrac{2a}{\left(c+a-b\right)\left(a+b-c\right)}=\dfrac{2a}{\left(b+c-a\right)\left(a+b+c\right)}\)
\(\Leftrightarrow a^2-\left(b-c\right)^2=\left(b+c\right)^2-a^2\)
\(\Leftrightarrow a^2=b^2+c^2\) hay tam giác ABC vuông tại A.
Vậy ta có điều phải chứng minh.

3: \(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+2\left(x>=\dfrac{1}{2}\right)\\2x-1=-x-2\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-\dfrac{1}{3}\left(nhận\right)\end{matrix}\right.\)
\(1,ĐK:x\ge1\\ PT\Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ 2,\Leftrightarrow2x-5=x^2-8x+16\left(x\ge4\right)\\ \Leftrightarrow x^2-10x+21=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=7\left(tm\right)\end{matrix}\right.\\ 3,\Leftrightarrow\left[{}\begin{matrix}2x-1=x+2\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+2\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{1}{3}\left(tm\right)\end{matrix}\right.\)

a: Để phương trình có nghiệm duy nhất thì \(\left(m-3\right)\left(m+2\right)< >0\)
hay \(m\notin\left\{3;-2\right\}\)
Để phương trình vô nghiệm thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+2\right)=0\\\left(m-3\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-2\)
Để phương trình có vô số nghiệm thì m=3

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...





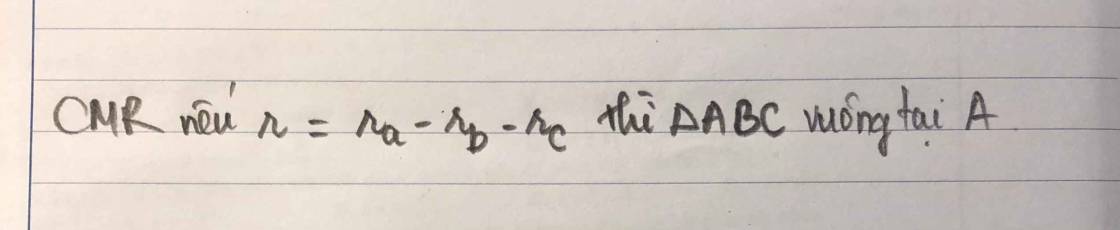


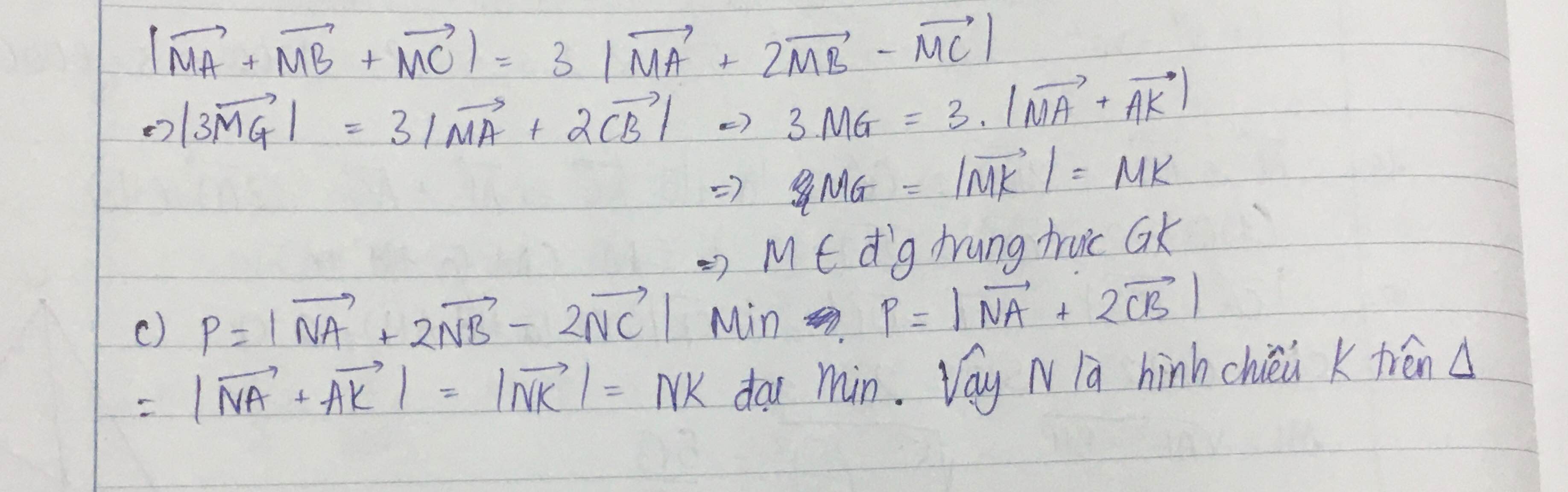 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.


1: \(\overrightarrow{AB}=\left(-3;-1\right)\)
\(\overrightarrow{AC}=\left(1;2\right)\)