Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: \(BE\cdot BA+CF\cdot CA+2\cdot BH\cdot CH\)
\(=BH^2+CH^2+2\cdot BH\cdot CH\)
\(=BC^2\)

Sửa đề: F là hình chiếu của E trên AC
a: Xét ΔCAB có
E là trung điểm của CB
EF//AB
=>F là trung điểm của AC
Xét ΔCAB có
E là trung điểm của CB
ED//AC
=>D là trung điểm của AB
Xét ΔABC có EF//AB
nên EF/Ab=CE/CB=1/2
=>EF=1/2AB=DB
Xét tứ giác BDFE có
FE//BD
FE=BD
=>BDFE là hình bình hành
b: Xét ΔABC có AD/AB=AF/AC
nên DF//BC
=>DF//EH
ΔHAC vuông tại H có HF là trung tuyến
nên HF=AC/2
=>HF=ED
Xét tứ giác EHDF có
EH//DF
ED=HF
=>EHDF là hình thang cân
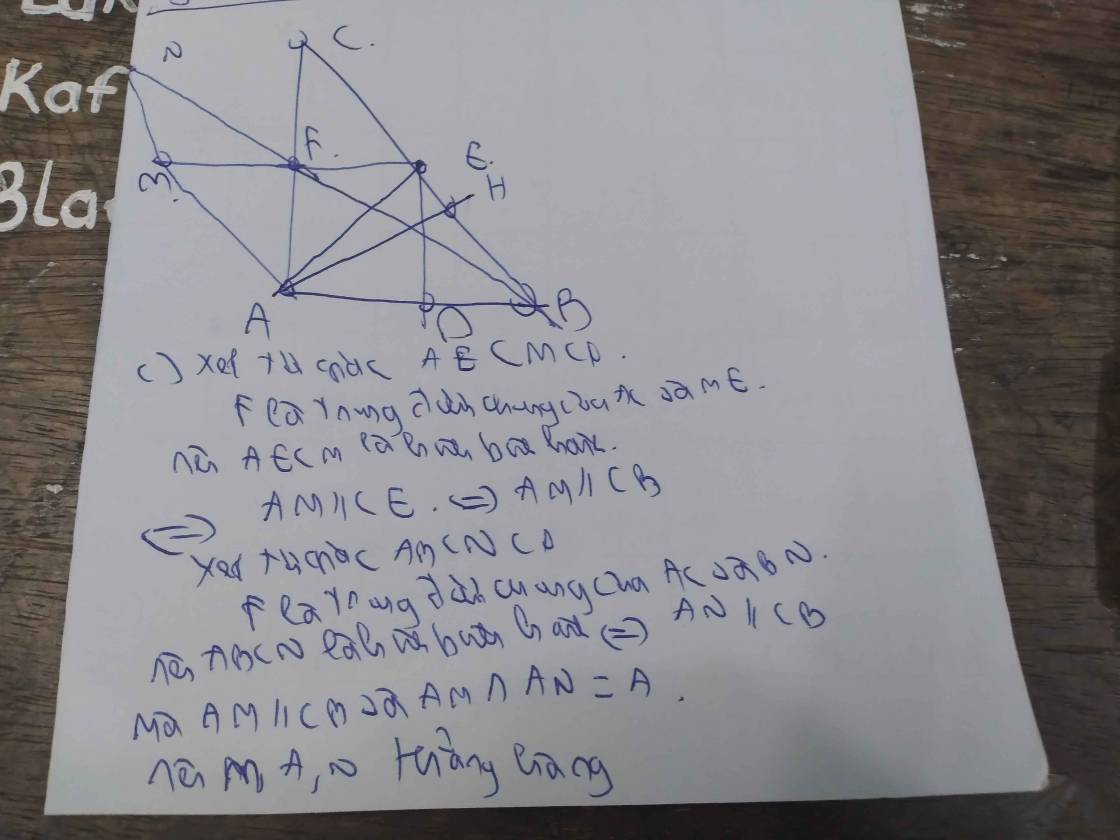
c: Xét tứ giác ABCN có
F là trung điểm chung của AC và BN
=>ABCN là hình bình hành
=>AN//CB
Xét tứ giác AMCE có
F là trung điểm chung của AC và ME
=>AMCE là hình bình hành
=>AM//CE
=>AM//CB
mà AN//CB
nên A,N,M thẳng hàng

a, Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow BC^2=64+225=289\Rightarrow BC=17\)cm
Xét tam giác AHC và tam giác BAC ta có :
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác AHC ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{AH}{AB}=\frac{AC}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\)cm
b, Vì MH vuông AB
NA vuông AB
=> MH // NA tương tự ta có : MH // AN
=> tứ giác AMNH là hình bình hành
mà ^HNA = 900 ; ^BAC = 900 ; ^HMA = 900
=> tứ giác AMHN là hình vuông

a, Xét tứ giác ADHE có :
^A = ^ADH = ^HEA = 900
Vậy tứ giác ADHE là hcn
Vậy AH = DE ( 2 đường chéo bằng nhau )
b, Xét tam giác AEH và tam giác AHC có :
^AEH = ^AHC = 900
^A _ chung
Vậy tam giác AEH ~ tam giác AHC ( g.g )
=> AH/AC = AE/AH => AH^2 = AE.AC (1)
tương tự với tam giác ADH ~ tam giác AHB (g.g)
=> AD/AH = AH/AB => AH^2=AD.AB (2)
Từ (1) ; (2) suy ra AE.AC = AD.AB
c, Xét tam giác ABH và tam giác CAH
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác ABH ~ tam giác CAH (g.g)
=> AH/CH = BH/AH => AH^2 = BH.CH
=> CH = AH^2/BH = 144/9 = 16
=> BC = BH + CH = 25 cm
Diện tích tam giác ABC là : SABC = 1/2 . AH . BC
= 1/2 . 12 . 25 = 150 cm2

a: XétΔAHB vuông tại H có HM là đường cao
nên BM*BA=BH^2; AM*AB=AH^2; HM*AB=HA*HB
Xét ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2; CN*CA=CH^2; HA*HC=HN*CA
CN*BM*BC
=BH^2/BA*CH^2/CA*BC
\(=\dfrac{\left(BH\cdot CH\right)^2}{BA\cdot CA}\cdot BC\)
=AH^4/AH=AH^3
AM*AB=AH^2
AN*AC=AH^2
=>AM*AB=AN*AC(Cái này mới đúng nè bạn, còn cái AM*AC=AN*AB là sai đề rồi á)
b: AM*AN
=AH^2/AB*AH^2/AC
=AH^4/AB*AC
\(=\dfrac{AH^4}{AH\cdot BC}=\dfrac{AH^3}{BC}\)
c: Sửa đề: AB^3/AC^3=BM/CN
\(\dfrac{BM}{CN}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}\)
\(=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)

a: Xét ΔHCA vuông tại H và ΔACB vuông tại A có
góc HCA chung
Do đó:ΔHCA\(\sim\)ΔACB
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\)
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
XétΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE