Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 3 của 4 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_4^3\) ( phần tử)
b) +) Sự kiện “Tổng các số trên ba tấm bìa bằng 9” tương ứng với biến cố \(A = \left\{ {\left( {4;3;2} \right)} \right\}\)
+) Sự kiện “Các số trên ba tấm bìa là ba số tự nhiên liên tiếp” tương ứng với biến cố \(B = \left\{ {\left( {1;2;3} \right),\left( {2;3;4} \right)} \right\}\)
c) +) Ta có: \(n\left( A \right) = 1\),\(n\left( B \right) = 2\)
+) Vậy xác suất của biến cố A và B là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

Đầu tiên, cứ gọi 2 sợi dây là A và B cho dễ nhé. Muốn giải được câu đố này, bạn phải dựa vào dữ kiện duy nhất được cung cấp: A và B đều cháy hết trong vòng 1 giờ đồng hồ khi đốt cháy một đầu.
Điều này có nghĩa là nếu đốt cháy 2 đầu, sợi dây sẽ cháy trong đúng 30 phút. Và sau khi cháy được một nửa, bạn đốt nốt đầu còn lại, thì khoảng thời gian cho đoạn dây còn lại cháy hết sẽ đúng bằng 15 phút.
Vậy vấn đề bây giờ chỉ là làm cách nào đo được chính xác thời điểm đoạn dây cháy còn một nửa mà thôi.
Dễ quá rồi đúng không: Với dây A, hãy đốt cháy 2 đầu, đồng thời đốt một đầu của dây B.

Đáp án của câu đố kinh điển trên.
Khi dây A cháy hết, dây B sẽ còn 30 phút nữa để cháy. Giờ hãy châm lửa vào đầu còn lại của dây B, và khi B cháy hết, chính xác 45 phút đã trôi qua.
nha hoc24

Gọi năng suất ban đầu là x, thời gian ban đầu là y
Theo đề, ta có hệ: xy=120 và 2x+(x+4)(y-2-1)-16=120
=>xy=120 và 2x+(x+4)(y-3)=136
=>xy=120 và 2x+xy-3x+4y-12=136
=>xy=120 và -x+4y+120-12=136
=>-x+4y=28 và xy=120
=>x=4y-28 và y(4y-28)=120
=>y=10 và x=4*10-28=12

\(M\left(Z_1,N_2\right)vaX\left(Z_2,N_2\right)\)
\(2Z_1+N_1+2Z_2+N_2=108\)
\(2\left(Z_1+Z_2\right)-\left(N_1+N_2\right)=36\)
\(Z_1+N_1-Z_2-N_2=8\)
\(2Z_1+N_1-2-\left(2Z_2+N_2+2\right)=8\)
Từ hệ trên

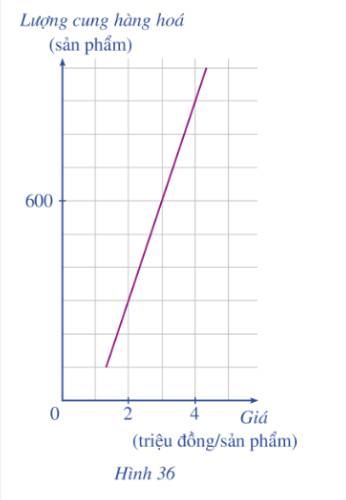
a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.
b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.
Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.