
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{2+\sqrt{2}}.\sqrt{2-\sqrt{2}}\)
\(=\sqrt{\left(2+\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{2^2-\left(\sqrt{2}\right)^2}=\sqrt{4-2}=\sqrt{2}\)


\(ĐK:\dfrac{2}{3x+5}\ge0\Leftrightarrow3x+5\ge0\left(2>0\right)\Leftrightarrow x\ge-\dfrac{5}{3}\)
\(ĐKXĐ:\left\{{}\begin{matrix}\dfrac{2}{3x+5}\ge0\\3x+5\ne0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+5\ge0\\x\ne-\dfrac{5}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{5}{3}\\x\ne-\dfrac{5}{3}\end{matrix}\right.\\ \Leftrightarrow x>-\dfrac{5}{3}\)

2 công nhân làm cùng cv trong 4 ngày
\(\rightarrow\)1 ngày làm 1/4 công việc
người thứ 1 làm mất 6 ngày
\(\rightarrow\)1 ngày làm 1/6 công việc
gọi a là số công việc người 2 lm trong 1 ngày
ta có pt \(\frac{1}{4}=\frac{1}{6}+a\)---> \(a=\frac{1}{12}\)
----> người 2 lm hết cv trong 12 ngày
mình ko hiểu câu hỏi b cko lắm

Câu II:
1: Thay m=3 vào y=(m-2)x+3, ta được:
\(y=\left(3-2\right)x+3=x+3\)
*Vẽ đồ thị:
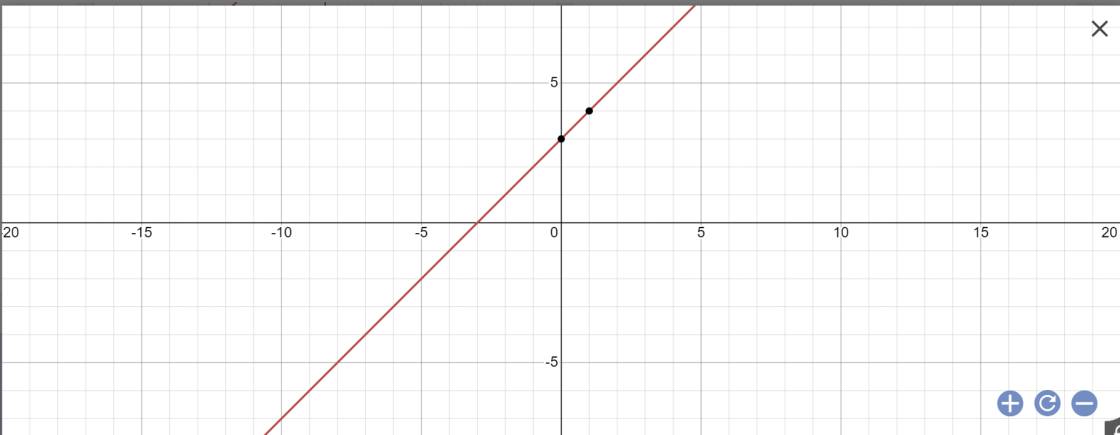
2: Để (d1) cắt (d2) tại một điểm trên trục tung thì:
\(\left\{{}\begin{matrix}m-2\ne-1\\m^2+2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m^2=1\end{matrix}\right.\)
=>m=-1
3: (d1): y=(m-2)x+3
=>(m-2)x-y+3=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\left(m-2\right)+0\cdot\left(-1\right)-3\right|}{\sqrt{\left(m-2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}\)
Để d(O;(d1))=3/2 thì \(\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{3}{2}\)
=>\(\sqrt{\left(m-2\right)^2+1}=2\)
=>(m-2)2+1=4
=>(m-2)2=3
=>\(m-2=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+2\)

Gọi chiều cao toa tháp là :BA
khoảng cách từ cậu bé đến tòa tháp là: AC
Xét tam giác ABC có : góc BAC = 90 độ
=> tan ABC = AB/AC
=> AB = tan ABC x AC
=> AB = tan 74 độ x 132
=> AB = sấp sỉ 480,33 ( m)
Chiều cao thục của tòa tháp là : 460,33 + 1,6 = 461,93 (m)

Đặt \(AB=a;AC=b\)
Xét \(\Delta ABC\) vuông tại A ta có :
Áp dụng hệ thức lượng trong \(\Delta\) vuông ta được :
\(\Leftrightarrow AH.BC=a.b\)
\(\Leftrightarrow ab=25.12=300\left(1\right)\)
Mặt khác:
Xét \(\Delta ABC\) vuông tại A, theo định lý Pytago ta được:
\(\Leftrightarrow a^2+b^2=BC^2\)
\(\Leftrightarrow a^2+b^2=625\)
\(\Leftrightarrow\left(a+b\right)^2-2ab=625\)
Thay \(\text{ab=}300\) vào ta được :
\(\Leftrightarrow\left(a+b\right)^2-600=625\)
\(\Leftrightarrow\left(a+b\right)^2=1225\)
\(\Rightarrow a+b=35\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) Giải phương trình ta được: \(\left\{{}\begin{matrix}a=15\\b=20\end{matrix}\right.\)
\(\Rightarrow AB=15;AC=20\)
Xét \(\Delta AHC\) vuông tại H, theo định lý Pytago ta được:
\(HC=\sqrt{AC^2-AH^2}=16\)
Ta có: \(AB.AC=AH.BC=12.25=300\left(1\right)\)
Lại có: \(AB^2+AC^2=BC^2=625\)
\(\Rightarrow\left(AB+AC\right)^2=AB^2+AC^2+2AB.AC=625+600=1225\)
\(\Rightarrow AB+AC=35\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AB,AC\) là nghiệm của pt \(x^2-35x+300=0\)
\(\Rightarrow\left(x-20\right)\left(x-15\right)=0\) mà \(AB< AC\Rightarrow\left\{{}\begin{matrix}AB=15\\AC=20\end{matrix}\right.\)
Ta có: \(AC^2=CH.CB\Rightarrow CH=\dfrac{AC^2}{CB}=\dfrac{20^2}{25}=16\)
\(\Rightarrow D\)

1: Xét ΔABC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(BC=\dfrac{AC}{\sin60^0}\)
\(=\dfrac{32\sqrt{3}}{3}\left(cm\right)\)
hay \(AB=\dfrac{16\sqrt{3}}{3}\left(cm\right)\)







\(\sqrt{\left(1-\sqrt{2}\right)^2}\sqrt{\left(1+\sqrt{2}\right)^2}\)
\(=\sqrt{\left(1-\sqrt{2}\right)^2\left(1+\sqrt{2}\right)^2}\)
\(=\sqrt{\left(1-2\right)^2}=\sqrt{\left(-1\right)^2}=1\)
Câu 21: D
Câu 15: \(=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)
Câu 11: \(=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{6}=\dfrac{3+\sqrt{3}}{6}\)