
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 4n - 3m tại m = 2 và n = -3
Thay m = 2 , n = -3 vào biểu thức ta được: 4. 2 - 3 . ( -3 ) = 8 - ( -9 ) = 8 + 9 = 17
b) 2m + 7m - 6 tại m = -1 và n = 2
Có n đâu mà làm -.-

8:
a: Xét tứ giác ADCF có
E là trungd diểm chung của AC và DF
=>ADCF là hbh
=>AD//CF và AD=CF
=>CF=DB
b: Xét ΔBDC và ΔFCD có
BD=CF
DC chung
BC=DF
=>ΔBDC=ΔFCD
c: Xét ΔABC có AD/AB=AE/AC=1/2
nên DE//BC và DE=1/2BC

Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

https://hoc24.vn/cau-hoi/.1685893843618 (hoặc bn vào link này cho nhanh cũng đc, mik giải rồi)

Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30



Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.



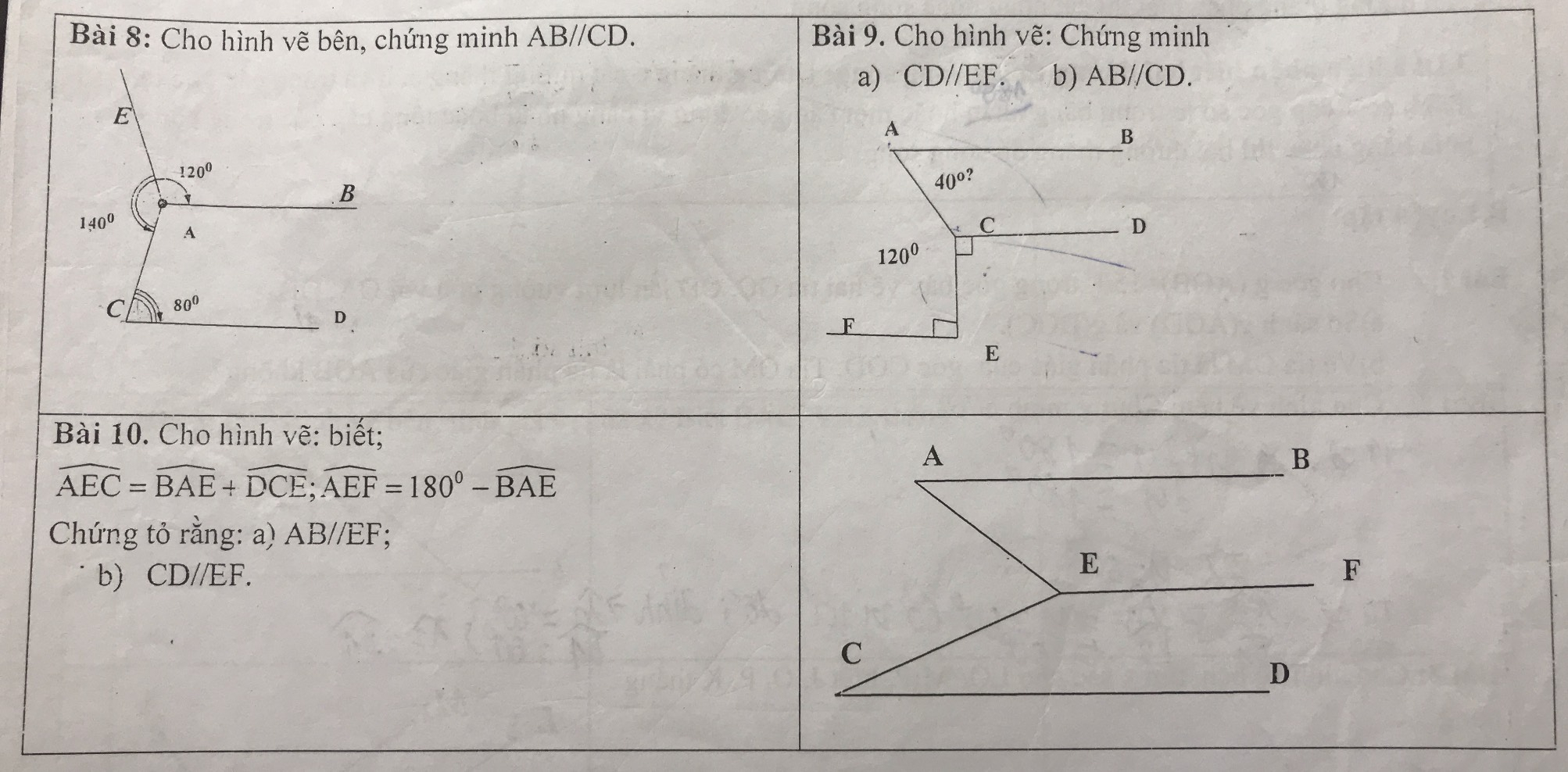 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi  lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!





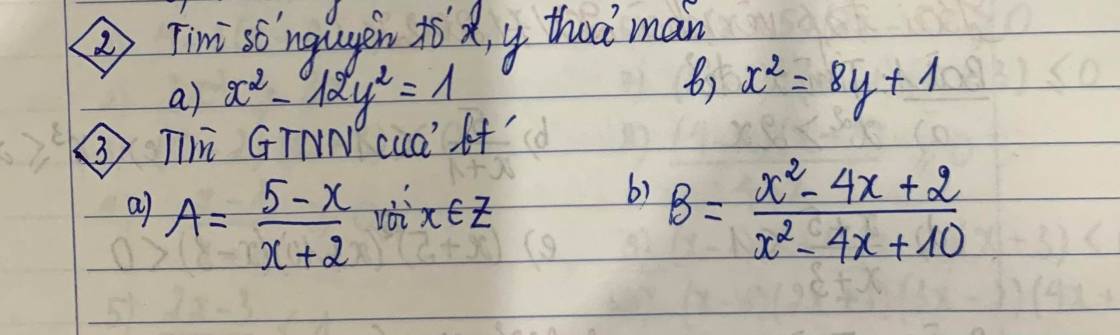
Bài 2 với bài 3 ạ
Câu 2: Kẻ đường thẳng d qua O song song với Mx
=> Góc dOM = góc M = 50o ( so le trong)
Vì Mx//Ny
=> d//Ny
Kéo dài yN, đặt T trên điểm kéo dài
Ta có: Góc ONT = 180o - 140o = 40o
=> Góc dON = góc ONT = 40o(so le trong)
=> Góc O = 40o + 50o = 90o