K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
5 tháng 3 2021
** Lần sau bạn chú ý viết đề bằng công thức toán để được hỗ trợ tốt hơn!
(biểu tượng $\sum$ ở góc màn hình bên trái)
Lời giải:\(\lim\limits_{x\to -\infty}(\sqrt[3]{6x^2-8x^3}+2x)=\lim\limits_{x\to -\infty}\frac{6x^2-8x^3+8x^3}{\sqrt[3]{(6x^2-8x^3)^2}-2x\sqrt[3]{6x^2-8x^3}+4x^2}\)
\(=\lim\limits_{x\to -\infty}\frac{6x^2}{\sqrt[3]{(6x^2-8x^3)^2}-2x\sqrt[3]{6x^2-8x^3}+4x^2}\)
\(=\lim\limits_{x\to -\infty}\frac{6}{\sqrt[3]{\frac{36}{x^2}-\frac{96}{x}+64}-2\sqrt[3]{\frac{6}{x}-8}+4}\)
\(=\frac{6}{\sqrt[3]{64}-2\sqrt[3]{-8}+4}=\frac{1}{2}\)
AH
Akai Haruma
Giáo viên
5 tháng 3 2021
** Lần sau bạn chú ý viết đề bằng công thức toán để được hỗ trợ tốt hơn!
(biểu tượng $\sum$ ở góc màn hình bên trái)
Lời giải:\(\lim\limits_{x\to -\infty}(\sqrt[3]{6x^2-8x^3}+2x)=\lim\limits_{x\to -\infty}\frac{6x^2-8x^3+8x^3}{\sqrt[3]{(6x^2-8x^3)^2}-2x\sqrt[3]{6x^2-8x^3}+4x^2}\)
\(=\lim\limits_{x\to -\infty}\frac{6x^2}{\sqrt[3]{(6x^2-8x^3)^2}-2x\sqrt[3]{6x^2-8x^3}+4x^2}\)
\(=\lim\limits_{x\to -\infty}\frac{6}{\sqrt[3]{\frac{36}{x^2}-\frac{96}{x}+64}-2\sqrt[3]{\frac{6}{x}-8}+4}\)
\(=\frac{6}{\sqrt[3]{64}-2\sqrt[3]{-8}+4}=\frac{1}{2}\)
MK
0
AH
Akai Haruma
Giáo viên
5 tháng 3 2021
*** Mình nhớ là đã nhắc nhở bạn về việc sử dụng hộp công thức toán để viết đề dễ hiểu hơn. Lần nữa thì mình xin phép xóa bài nhé. Bạn sử dụng bộ gõ công thức toán ở biểu tượng $\sum$
Lời giải:
\(\lim\limits_{x\to +\infty}(\sqrt[3]{x^3+5x}-\sqrt{x^2-3x+6})=\lim\limits_{x\to +\infty}[(\sqrt[3]{x^3+5x}-x)-(\sqrt{x^2-3x+6}-x)]\)
\(=\lim\limits_{x\to +\infty}\left[\frac{5x}{\sqrt[3]{(x^3+5x)^2}+x\sqrt[3]{x^3+5x}+x^2}-\frac{-3x+6}{\sqrt{x^2-3x+6}+x}\right]\)
\(=\lim\limits_{x\to +\infty}[\frac{5}{\sqrt[3]{x^3+10x+\frac{25}{x}}+\sqrt[3]{x^2+5x}+x}-\frac{-3+\frac{6}{x}}{\sqrt{1-\frac{3}{x}+\frac{6}{x^2}}+1}]\)
\(=(0-\frac{-3}{2})=\frac{3}{2}\)
ML
25 tháng 2 2022
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+x}-x\right)\\ =\lim\limits_{x→-\infty}\dfrac{x^3+x-x^3}{\left(\sqrt[3]{x^3+x}\right)^2+x\sqrt[3]{x^3+x}+x^2}\\ =\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{1}{x}}{\left(\sqrt[3]{1+\dfrac{1}{x^2}}\right)^2+\sqrt{1+\dfrac{1}{x^2}}+1}\\ =\lim\limits_{x\rightarrow-\infty}\dfrac{0}{1^2+1+1}=0\)
PN
1
DD
Đoàn Đức Hà
Giáo viên
28 tháng 3 2021
\(lim\left(\sqrt{mx^2+nx+20}-3x\right)=lim\frac{mx^2+nx+20-9x^2}{\sqrt{mx^2+nx+20}+3x}\)
\(=lim\frac{\left(m-9\right)x^2+nx+20}{\sqrt{mx^2+nx+20}+3x}=lim\frac{\left(m-9\right)x+n+\frac{20}{x}}{\sqrt{m+\frac{n}{x}+\frac{20}{x^2}}+3}=\frac{8}{3}\)
\(\Leftrightarrow\hept{\begin{cases}m-9=0\\\frac{n}{\sqrt{m}+3}=\frac{8}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}m=9\\n=16\end{cases}}\).
26 tháng 12 2023
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{4x^2+x}+2x-1\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{4x^2+x-\left(2x-1\right)^2}{\sqrt{4x^2+x}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{4x^2+x-4x^2+4x-1}{\sqrt{4x^2+x}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5x-1}{-x\cdot\sqrt{4+\dfrac{1}{x}}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5-\dfrac{1}{x}}{-\sqrt{4+\dfrac{1}{x}}-2+\dfrac{1}{x}}\)
\(=\dfrac{5-0}{-\sqrt{4+0}-2+0}=\dfrac{5}{-4}=-\dfrac{5}{4}\)
AH
Akai Haruma
Giáo viên
12 tháng 3 2020
a.
\(\lim\limits_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}=\lim_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{(x-1)^3(3x+1)}=\lim\limits _{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x+1}.\lim\limits_{x\to 1+}\frac{1}{(x-1)^3}\)
\(=\frac{1}{4}.(+\infty)=+\infty \)
Hoàn toàn tương tự:
\(\lim\limits_{x\to 1-}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}=-\infty \)
Do đó: \(\lim\limits_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\neq \lim\limits_{x\to 1-}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\) nên không tồn tại \(\lim\limits_{x\to 1}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\)
AH
Akai Haruma
Giáo viên
12 tháng 3 2020
b.
\(\lim\limits_{x\to 1+}\frac{x^3-3x^2+2}{x^4-4x+3}=\lim\limits_{x\to 1+}\frac{(x-1)(x^2-2x-2)}{(x-1)^2(x^2+2x+3)}=\lim\limits_{x\to 1+}\frac{x^2-2x-2}{(x-1)(x^2+2x+3)}\)
\(=\lim\limits_{x\to 1+}\frac{x^2-2x-2}{x^2+2x+3}.\lim\limits_{x\to 1+}\frac{1}{x-1}=\frac{-1}{2}.(+\infty)=-\infty \)
Tương tự \(\lim\limits_{x\to 1-}\frac{x^3-3x^2+2}{x^4-4x+3}=+\infty \)
Do đó không tồn tại \(\lim\limits_{x\to 1}\frac{x^3-3x^2+2}{x^4-4x+3}\)
c.
\(\lim\limits_{x\to 1}\frac{x^3-2x-1}{x^5-2x-1}=\frac{1^3-2.1-1}{1^5-2.1-1}=1\)
d.
\(\lim\limits_{x\to -1}\frac{(x+2)^2-1}{x^2-1}=\lim\limits_{x\to -1}\frac{(x+2-1)(x+2+1)}{(x-1)(x+1)}=\lim\limits_{x\to -1}\frac{x+3}{x-1}=-1\)
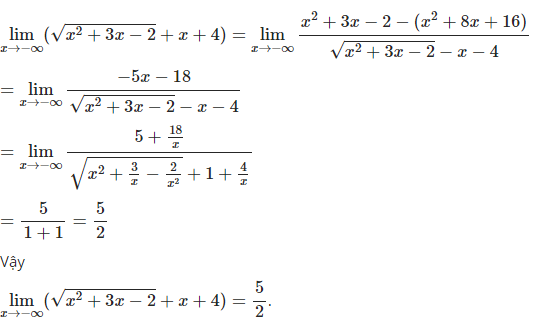
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{6x^2}{\sqrt[3]{\left(6x^2-8x^3\right)^2}-2x\sqrt[3]{6x^2-8x^3}+4x^2}=\dfrac{3}{2}\)
Kết quả bằnt 1/2 í bạn 🥺