Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(-1\le sin\left(1,5t+\dfrac{\pi}{3}\right)\le1\Leftrightarrow-3\le-3sin\left(1,5t+\dfrac{\pi}{3}\right)\le3\Leftrightarrow-3\le v\le3\)
a, Vận tốc con lắc đạt giá trị lớn nhất khi
\(-3sin\left(1,5t+\dfrac{\pi}{3}\right)=3\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=-1\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=sin\left(-\dfrac{\pi}{2}\right)\\ \Leftrightarrow\left[{}\begin{matrix}1,5t+\dfrac{\pi}{3}=-\dfrac{\pi}{2}+k2\pi\\1,5t+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\Leftrightarrow t=-\dfrac{5\pi}{9}+\dfrac{k4\pi}{3},k\in Z\)
Vậy vận tốc con lắc đạt giá trị lớn nhất tại các thời điểm \(t=-\dfrac{5\pi}{9}+\dfrac{k4\pi}{3},k\in Z\)
b, Để vận tốc con lắc bằng 1,5cm/s thì
\(-3sin\left(1,5t+\dfrac{\pi}{3}\right)=1,5\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\\ \)
\(\Leftrightarrow\left[{}\begin{matrix}1,5t+\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\1,5t+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\\ \)
\(\Leftrightarrow \left[{}\begin{matrix}t=-\dfrac{\pi}{3}+\dfrac{k4\pi}{3}\\t=\dfrac{5\pi}{9}+\dfrac{k4\pi}{3}\end{matrix}\right.\) \(\left(k\in Z\right)\)

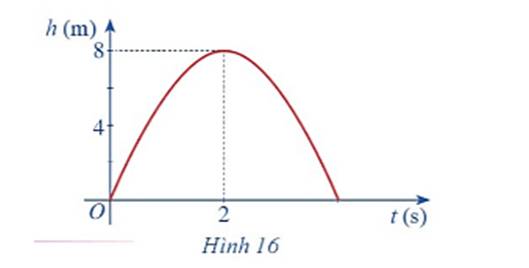
a) Hàm số \(h\left( t \right) = - 2{t^2} + 8t\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) do đó hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hàm số khi t tiến dần đến 2 thì h(t) dần đến 8.
Vậy \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right) = 8\)

Dùng định nghĩa ta tính được Q'(t) = 4t + 1, từ đó suy ra cường độ dòng điện tại thời điểm t = 4(s) là I(4) = Q'(4) = 4.4 + 1 = 17
Chọn D

Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

Vận tốc tại thời điểm t là \(v\left( t \right) = s'\left( t \right) = 0,5.2\pi \cos \left( {2\pi t + \frac{\pi }{5}} \right) = \pi \cos \left( {2\pi t + \frac{\pi }{5}} \right)\)
Gia tốc tức thời của vật tại thời điểm t là \(a\left( t \right) = v'\left( t \right) = - \pi .2\pi \sin \left( {2\pi t + \frac{\pi }{5}} \right) = - 2{\pi ^2}\sin \left( {2\pi t + \frac{\pi }{5}} \right)\)
Tại thời điểm t = 5 giây, gia tốc của vật là \(a\left( 5 \right) = - 2{\pi ^2}\sin \left( {2\pi .5 + \frac{\pi }{5}} \right) \approx - 11,6\)(cm/s2)

Ta có: \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) = 2\left[ {\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)} \right]\)
\(2\left[ {\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} + \frac{\pi }{3}t - \frac{\pi }{3}}}{2}} \right).\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} - \frac{\pi }{3}t + \frac{\pi }{3}}}{2}} \right)} \right] = 2\left[2. {\cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right).\cos \frac{\pi }{4}} \right] = 2\sqrt 2 \cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right)\)
Vậy biên độ là \(2\sqrt 2 \), pha ban đầu \( - \frac{\pi }{{12}}\)

Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.

Vận tốc tức thời của chuyển động tại \(t = 2\) là:
\(\begin{array}{l}v\left( 2 \right) = s'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{s\left( t \right) - s\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{\left( {4{t^3} + 6t + 2} \right) - \left( {{{4.2}^3} + 6.2 + 2} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t + 2 - 46}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t - 44}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{2\left( {t - 2} \right)\left( {2{t^2} + 4t + 11} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} 2\left( {2{t^2} + 4t + 11} \right) = 2\left( {{{2.2}^2} + 4.2 + 11} \right) = 54\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = 54\left( {m/s} \right)\)

$[v(t) = \frac{ds(t)}{dt} = \frac{d}{dt}(2t^3+4t+1)]$
$[a(t) = \frac{dv(t)}{dt} = \frac{d}{dt}(6t^2 + 4)]$
$[a(t) = 12t]$
Khi (t = 1), ta có:
$[v(1) = 6(1)^2 + 4 = 10 , \text{m/s}]$4
$[a(1) = 12(1) = 12 , \text{m/s}^2]$
Vậy, khi (t = 1), vận tốc của vật là 10 m/s và gia tốc của vật là $12 m/s$

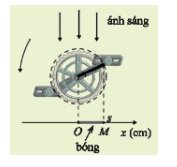
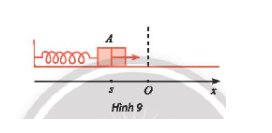
Ta có: \(s\in\left[-1;1\right]\Leftrightarrow-1\le2cos\left(\pi t\right)\le1\\ \Leftrightarrow-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\)
Trong 1s đầu tiên \(0< t< 1\Rightarrow0< \pi t< \pi\)
Ta có đồ thị hàm số \(y=cos\left(x\right)\) trên \(\left[0;\pi\right]\)
Dựa vào đồ thị, ta thấy
\(-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\Leftrightarrow\dfrac{\pi}{3}\le\pi t\le\dfrac{2\pi}{3}\Leftrightarrow\dfrac{1}{3}\le t\le\dfrac{2}{3}\)
Vậy \(t\in\left[\dfrac{1}{3};\dfrac{2}{3}\right]\)