Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)
Do đường tròn tiếp xúc với \(d_1;d_2\) nên:
\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)
Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.
2.
Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?
ĐÁP ÁN D
Tọa độ giao điểm của đường thẳng ∆ và đường tròn (C) nếu có là nghiệm hệ phương trình: là nghiệm của hệ phương trình
x − y + 4 = 0 ( 1 ) x 2 + y 2 + 2 x − 4 y − 8 = 0 ( 2 )
Từ (1) suy ra: y = x + 4 thay vào (2) ta được:
x 2 + ( x + 4 ) 2 + 2 x – 4 . ( x + 4 ) - 8 = 0 x 2 + x 2 + 8 x + 16 + 2 x - 4 x – 16 - 8 = 0
2x2 + 6x - 8 = 0 ⇔ x = 1 ⇒ y = 5 x = − 4 ⇒ y = 0
Vậy đường thẳng cắt đường tròn tại 2 điểm phân biệt là (1; 5) và ( -4; 0)
Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
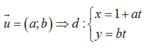
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
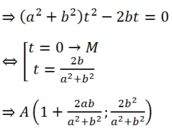
- Nếu d cắt (C2) tại B:
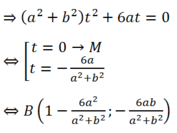
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
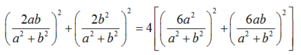
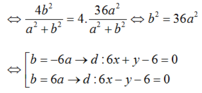
Đáp án: C
Ta có:
(C): x 2 + y 2 + 2x + 4y = 0 ⇔ (x + 1 ) 2 + (y + 2 ) 2 = 5
⇒ I(-1;-2), R = 5
Vì d’ song song với d nên d': 2x + y + c = 0, (c ≠ -3)
Đường thẳng d’ tiếp xúc với (C) nên
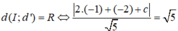
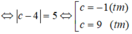
Vậy phương trình đường thẳng d’ là: 2x + y - 1 = 0 hoặc 2x + y + 9 = 0
ĐÁP ÁN D
Đường tròn (C) có tâm I( -1; 3).
Do đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB nên I M ⊥ Δ ( quan hệ vuông góc đường kính và dây cung).
Đường thẳng ∆: đi qua M(-2; 1) và nhận M I → ( 1 ; 2 ) làm VTPT nên có phương trình là :
1. (x + 2) + 2(y – 1) = 0 hay x+ 2y = 0
\(x-7y+10=0\Rightarrow x=7y-10\)
Thay vào pt đường tròn:
\(\left(7y-10\right)^2+y^2-2\left(7y-10\right)+4y-20=0\)
\(\Leftrightarrow y^2-3y+2=0\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-3\\y=2\Rightarrow x=4\end{matrix}\right.\)
Gọi \(B\left(-3;1\right);C\left(4;2\right)\)
Phương trình trung trực AB có dạng:
\(4\left(x+1\right)-3\left(y+\frac{1}{2}\right)=0\Leftrightarrow8x-6y+5=0\)
Phương trình trung trực BC có dạng:
\(7\left(x-\frac{1}{2}\right)+1\left(y-\frac{3}{2}\right)=0\Leftrightarrow7x+y-5=0\)
Tọa độ tâm I là nghiệm: \(\left\{{}\begin{matrix}8x-6y+5=0\\7x+y-5=0\end{matrix}\right.\) \(\Rightarrow I\left(\frac{1}{2};\frac{3}{2}\right)\)
\(\Rightarrow R^2=IA^2=\sqrt{\left(1-\frac{1}{2}\right)^2+\left(-2-\frac{3}{2}\right)^2}=\frac{25}{2}\)
Phương trình: \(\left(x-\frac{1}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=\frac{25}{2}\)
Quy trình làm như vậy, còn các bước tính toán bạn kiểm tra lại
Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau
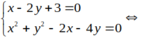
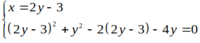
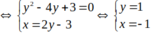hoặc 
Vậy tọa độ giao điểm là (3;3) và (-1; 1) .
Chọn A.
a) x2 + y2 – 4x + 8y – 5 = 0
⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25
⇔ (x – 2)2 + (y + 4)2 = 25.
Vậy (C) có tâm I(2 ; –4), bán kính R = 5.
b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:
(–1 – 2)2 + (0 + 4)2 = 32 + 42 = 52= R2
⇒ A thuộc đường tròn (C)
⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A
⇒ (d’) là đường thẳng đi qua A và vuông góc với IA
⇒ (d’) nhận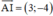 
là một vtpt và đi qua A(–1; 0)
⇒ phương trình (d’): 3(x + 1) – 4(y - 0)= 0 hay 3x – 4y + 3 = 0.
c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).
(d) có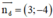 
là một vtpt; 1 VTCP là ud→(4; 3)
(Δ) ⊥ (d) ⇒ (Δ) nhận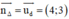 
là một vtpt
⇒ (Δ): 4x + 3y + c = 0.
(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R
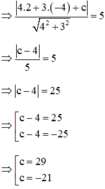
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.
Do đường tròn (C) đi qua M, N nên tâm I của đường tròn nằm trên trung trực của MN
Gọi P là trung điểm MN \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{NM}=\left(1;-2\right)\\P\left(\dfrac{3}{2};2\right)\end{matrix}\right.\)
Phương trình trung trực \(d_1\) của MN vuông góc MN và qua P có dạng
\(1\left(x-\dfrac{3}{2}\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+\dfrac{5}{2}=0\)
\(\Rightarrow\) Tọa độ I là nghiệm:
\(\left\{{}\begin{matrix}3x+7y+1=0\\x-2y+\dfrac{5}{2}=0\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{3}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow R^2=IM^2=\left(2+\dfrac{3}{2}\right)^2+\left(1-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)
Phương trình:
\(\left(x+\dfrac{3}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)
Tham khảo :
mk tham khảo nên ko chắc đúng
\(Đáp án: ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 Giải thích các bước giải: Tọa độ giao điểm của (d) và (C) là nghiệm của hệ phương trình { x − 7 y + 10 = 0 x 2 + y 2 − 2 x + 4 y − 20 = 0 ⇔ { x = 7 y − 10 ( 1 ) x 2 + y 2 − 2 x + 4 y − 20 = 0 ( 2 ) Thay (1) vào (2) ta được ( 7 y − 10 ) 2 + y 2 − 2 ( 7 y − 10 ) + 4 y − 20 = 0 ⇔ 49 y 2 − 140 y + 100 + y 2 − 14 y + 20 + 4 y − 20 = 0 ⇔ 50 y 2 − 150 y + 100 = 0 ⇔ y 2 − 3 y + 2 = 0 ⇔ ( y − 2 ) ( y − 1 ) = 0 ⇔ [ y = 2 y = 1 + ) y = 2 ⇒ x = 4 ⇒ B ( 4 ; 2 ) + ) y = 1 ⇒ x = − 3 ⇒ C ( − 3 ; 1 ) Phương trình đường tròn có dạng ( C 1 ) x 2 + y 2 − 2 a x − 2 b y + c = 0 Ta có đường tròn đi qua 3 điểm A ( 1 ; − 2 ) , B ( 4 ; 2 ) , C ( − 3 ; 1 ) A ( 1 ; − 2 ) ∈ ( C 1 ) : 1 2 + ( − 2 ) 2 − 2 a + 4 b + c = 0 ⇔ − 2 a + 4 b + c = − 5 B ( 4 ; 2 ) ∈ ( C 1 ) : 4 2 + 2 2 − 8 a − 4 b + c = 0 ⇔ − 8 a − 4 b + c = − 20 C ( − 3 ; 1 ) ∈ ( C 1 ) : ( − 3 ) 2 + 1 2 + 6 a − 2 b + c = 0 ⇔ 6 a − 2 b + c = − 10 Ta có hệ phương trình ⎧ ⎨ ⎩ − 2 a + 4 b + c = − 5 − 8 a − 4 b + c = − 20 6 a − 2 b + c = − 10 ⇔ ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ a = 1 2 b = 3 2 c = − 10 ⇒ I ( 1 2 ; 3 2 ) , R = √ 1 2 2 + 3 2 2 − ( − 10 ) = 5 √ 2 2 Phương trình đường tròn có dạng ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 \)
Xucana nó lỗi luôn😂