
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3) \(\frac{x}{9}=\frac{y}{12}=\frac{z}{16}\)
=> \(\frac{3x}{27}=\frac{2y}{24}=\frac{z}{16}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{3x}{27}=\frac{2y}{24}=\frac{z}{16}=\frac{3x+2y-z}{27+24-16}=\frac{13}{35}\)
=> \(\begin{cases}x=\frac{13}{35}.9=\frac{117}{35}\\y=\frac{13}{35}.12=\frac{156}{35}\\z=\frac{208}{35}\end{cases}\)
4) Ta có:
3.81 = 9.27
Vậy ta lập được các tỉ lệ thức là:
\(\frac{3}{9}=\frac{27}{81};\frac{3}{27}=\frac{9}{81};\frac{81}{9}=\frac{27}{3};\frac{81}{27}=\frac{9}{3}\)

Ta có : \(\frac{\widehat{A}}{3}=\widehat{\frac{B}{4}}=\frac{\widehat{C}}{8}\) và \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\widehat{\frac{A}{3}}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{8}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+4+8}=\frac{180}{15}=12\)
\(\Rightarrow\begin{cases}\frac{\widehat{A}}{3}=12\Rightarrow\widehat{A}=36^0\\\frac{\widehat{B}}{4}=12\Rightarrow\widehat{B}=48^0\\\frac{\widehat{C}}{8}=12\Rightarrow\widehat{C}=96^0\end{cases}\)
Vậy ..................

Theo bài ra ta có :
\(x:y:z=5:\left(-3\right):8\)
\(\frac{x}{5}=\frac{y}{-3}=\frac{z}{8}\)
\(\Rightarrow\frac{3x}{15}=\frac{5y}{-15}=\frac{2z}{16}\)
\(\Rightarrow\frac{3x-5y-2x}{15-\left(-15\right)-16}=\frac{42}{14}\)
\(\Rightarrow x=3.5=15\)
\(\Rightarrow y=-3.3=-9\)
\(\Rightarrow z=8.3=24\)
mấy cái còn lại tương tự thôi nha bạn :))

Gọi số học sinh giỏi , khá , trung bình , yếu là : a , b , c , d ( a,b,c,d > 0 )
Theo bài ra , ta có :
\(\frac{a}{9}=\frac{b}{11}=\frac{c}{13}=\frac{d}{3}\)
và b - a = 20
Áp dụng dãy tỉ số bằng nhau , ta có :
\(\frac{b-a}{11-9}=\frac{20}{2}=10\)
- \(\frac{a}{9}=10\Rightarrow a=10.9=90\left(hs\right)\)
- \(\frac{b}{11}=10\Rightarrow b=11.10=110\left(hs\right)\)
- \(\frac{c}{13}=10\Rightarrow c=10.13=130\left(hs\right)\)
- \(\frac{d}{3}=10\Rightarrow d=10.3=30\left(hs\right)\)
Vậy có 90 HSG : 110 HSK ; 130 HSTB ; 30 HSY

Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$

\(\dfrac{\left(-3\right)^2.3^3.625}{\left(-5\right)^6.\left|-81\right|}=\dfrac{3^2.3^3.5^4}{5^6.81}=\dfrac{3^5.5^4}{5^6.3^4}=\dfrac{3}{5^2}=\dfrac{3}{25}\)

 và
và


 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
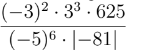 cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !
cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !
không có đề làm bằng niềm tin ak bạn
nói cộc lốc zậy sao mà bik giúp bn dk nhệ