
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: Ta có: \(12x^2+7x-12\)
\(=12x^2+16x-9x-12\)
\(=4x\left(3x+4\right)-3\left(3x+4\right)\)
\(=\left(3x+4\right)\left(4x-3\right)\)
e: Ta có: \(15x^2+7x-2\)
\(=15x^2+10x-3x-2\)
\(=\left(3x+2\right)\left(5x-1\right)\)

\(a^{2k}-b^{2k}=\left(a+b\right)\left(a^{2k-1}-a^{2k-2}b+a^{2k-3}b^2-....-a^2b^{2k-3}+ab^{2k-2}-b^{2k-1}\right)\)
Tam giác pascal: 1
1 2 1
1 3 3 1
1 4 6 4 1

\(d,\left(2x-1\right)\left(x+3\right)+2x\left(2-x\right)=10-8\left(x+4\right)\\ \Leftrightarrow2x^2+6x-x-3+4x-2x^2=10-8x-32\\ \Leftrightarrow17x=19\Leftrightarrow x=\dfrac{19}{17}\)
vậy phương trình đã cho có nhiệm \(x=\dfrac{19}{17}\)
Ta có: \(\left(2x-1\right)\left(x+3\right)+2x\left(2-x\right)=10-8\left(x+4\right)\)
\(\Leftrightarrow2x^2+6x-x-3+4x-2x^2=-8x-22\)
\(\Leftrightarrow18x=-19\)
hay \(x=-\dfrac{19}{18}\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)


Gọi \(x\) ngày) là thời gian để người thứ nhất làm xong công việc \((x>0)\)
Một ngày người thứ nhất làm được \(\dfrac{1}{2}\left(cv\right)\)
Một ngày người thứ hai làm được \(\dfrac{2}{3}.\dfrac{1}{x}=\dfrac{2}{3x}\left(cv\right)\)
Cả hai người làm chung trong 1 ngày được: \(\dfrac{1}{x}+\dfrac{2}{3x}\left(cv\right)\)
Ta có ,Phương trình :
\(\dfrac{1}{x}+\dfrac{2}{3x}=\dfrac{1}{12}\)
\(12 + 8 = x\)
\(⇔ x = 20 ( t m )\)
Người thứ nhất làm xong công việc trong \(20ng\) ; người thứ hai làm xong công việc trong \(20.\dfrac{3}{2}=30ng\)

\(f,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow4x^4-13x^3+23x^2+18x-k=\left(x+4\right)\cdot c\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow4\cdot\left(-4\right)^4-13\cdot\left(-4\right)^3+23\cdot\left(-4\right)^2+18\left(-4\right)-k=0\\ \Leftrightarrow1024+832+368-72-k=0\\ \Leftrightarrow k=2152\)
\(d,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow x^4-8x^3+24x^2+7x+k=\left(x+4\right)\cdot a\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow\left(-4\right)^4-8\left(-4\right)^3+24\left(-4\right)^2+7\left(-4\right)+k=0\\ \Leftrightarrow256+512+384-28+k=0\\ \Leftrightarrow k=-1124\)

\(a.\) Từ \(x-2y=1\) \(\Rightarrow\) \(x=1+2y\) \(\left(\text{*}\right)\)
Thay \(x=1+2y\) vào \(A\), khi đó, biểu thức \(A\) trở thành
\(A=\left(1+2y\right)^2+y^2+4=1+4y+4y^2+y^2+4=5y^2+4y+5\)
\(A=5\left(y^2+\frac{4}{5}y+1\right)=5\left(y^2+2.\frac{2}{5}.y+\frac{4}{25}+\frac{21}{25}\right)=5\left(y+\frac{2}{5}\right)^2+\frac{21}{5}\ge\frac{21}{5}\) với mọi \(y\)
Dấu \(''=''\) xảy ra \(\Leftrightarrow\) \(\left(y+\frac{2}{5}\right)^2=0\) \(\Leftrightarrow\) \(y+\frac{2}{5}=0\) \(\Leftrightarrow\) \(y=-\frac{2}{5}\)
Thay \(y=-\frac{2}{5}\) vào \(\left(\text{*}\right)\), ta được \(x=\frac{1}{5}\)
Vậy, \(A\) đạt giá trị nhỏ nhất là \(A_{min}=\frac{21}{5}\) khi và chỉ khi \(x=\frac{1}{5}\) và \(y=-\frac{2}{5}\)
\(b.\) Gọi \(Q\left(x\right)\) là thương của phép chia và dư là \(r=ax+b\) (vì dư trong phép chia cho \(x^2-1\) có bậc cao nhất là bậc nhất), với mọi \(x\) ta có:
\(x^{2008}-x^3+5=\left(x^2-1\right).Q\left(x\right)+ax+b\) \(\left(\text{**}\right)\)
Với \(x=1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(5=a+b\) \(\left(1\right)\)
Với \(x=-1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(7=-a+b\) \(\left(2\right)\)
Giải hệ phương trình \(\left(1\right)\) và \(\left(2\right)\), ta được \(a=-1\) và \(b=6\)
Vậy, dư trong phép chia đa thức \(x^{2008}-x^3+5\) cho đa thức \(x^2-1\) là \(-x+6\)
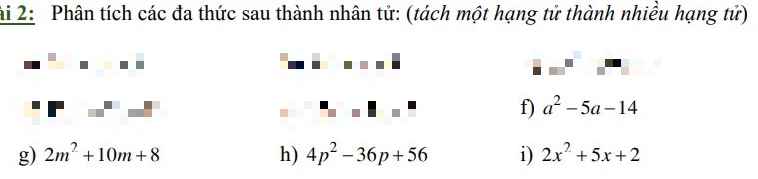

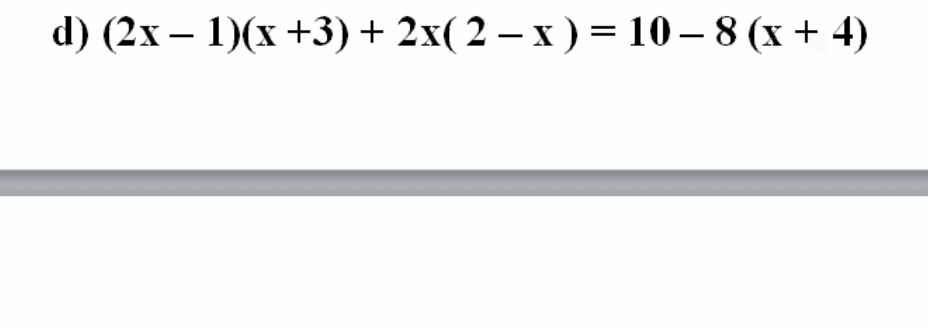 Giúp em vs ạ ! Em camon.
Giúp em vs ạ ! Em camon. 

Bài này dài, bn dùng pp thêm bớt rồi giải bằng hằng đẳng thức nha
mk không giúp đc xl