
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: AH=căn 9*16=12cm
AC=căn 12^2+16^2=20cm
HK=16*12/20=192/20=9,6cm
5:
a: Xét ΔMNP vuông tại N và ΔMHN vuông tại H có
góc M chung
=>ΔMNP đồng dạng với ΔMHN
b: NH=căn 16*9=12cm
NP=căn 16^2+12^2=20cm
HK=16*12/20=192/20=9,6cm

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

Bài 3:
\(b,\Leftrightarrow\left(x+8\right)\left(x+8-3x\right)=0\\ \Leftrightarrow\left(x+8\right)\left(8-2x\right)=0\\ \Leftrightarrow2\left(4-x\right)\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

a: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
Suy ra: AH=DE
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
c: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay AD/AC=AE/AB
Xét ΔADE vuông tại A và ΔACB vuông tại A có
AD/AC=AE/AB
Do đó: ΔADE\(\sim\)ΔACB

a: \(=4x^2-x^4+8-2x^2=-x^4+2x^2+8\)
b: \(=\dfrac{x^2+x}{x+1}=x\)

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

a) x^2 - x = 0
x(x-1)=0
x=0 hoặc x=1
b) (x-2)^2 - 3(x-2)=0
(x-2)(x-5)=0
x=2 hoặc x=5
c) pt <=> 3(x - 1) - 2(x - 1)=0
<=> x-1=0
<=> x = 1
a) \(\Rightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-2\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(\Rightarrow3\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow x-1=0\Rightarrow x=1\)
d) \(\Rightarrow\left(x-5\right)\left(x+5\right)+\left(x-5\right)^2=0\)
\(\Rightarrow\left(x-5\right).2x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
e) \(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)
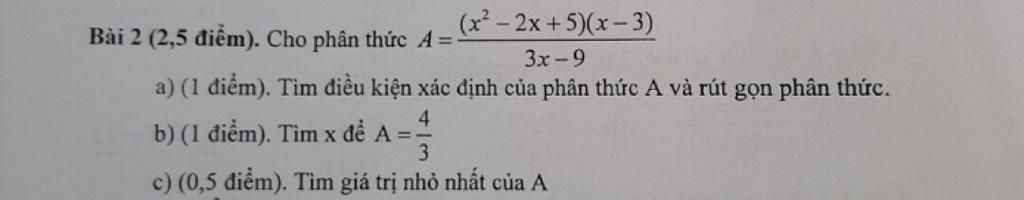


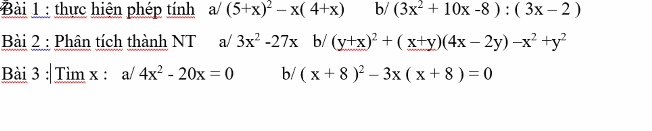




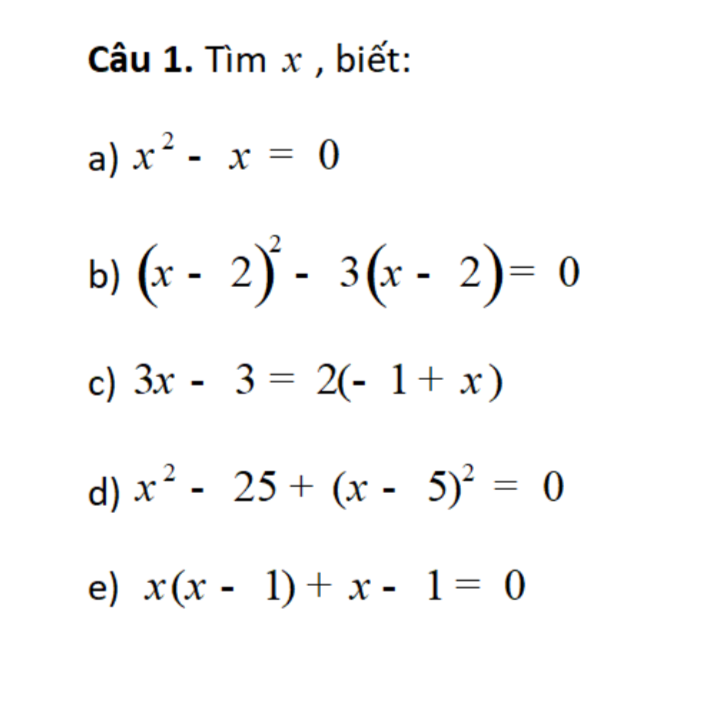

a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)