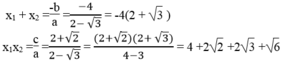Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(2x^2-3x-2=0\)
nên a=2; b=-3 và c=-2
Vì \(x_1\) và \(x_2\) là nghiệm của phương trình \(2x^2-3x-2=0\) nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{3}{2}\\x_1\cdot x_2=-\dfrac{2}{2}=-1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=-1\)
nên \(2\cdot x_1\cdot x_2=-2\)
Ta có: \(\left(x_1+x_2\right)^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2+2\cdot x_1\cdot x_2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2=\dfrac{9}{4}+2=\dfrac{17}{4}\)

2x2 – 17x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b2 – 4ac = (-17)2 – 4.2.1 = 281 > 0.
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x1 + x2 = -b/a = 17/2
x1.x2 = c/a = 1/2.

Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1+y_2=2x_1-x_2+2x_2-x_1\\y_1y_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1+x_2\\y_1y_2=-2x_1^2-2x_2^2+5x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2\left(x_1+x_2\right)^2+9x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2.\left(-\dfrac{5}{3}\right)^2+9.\left(-2\right)=-\dfrac{212}{9}\end{matrix}\right.\)
\(\Rightarrow y_1;y_2\) là nghiệm của:
\(y^2+\dfrac{5}{3}y-\dfrac{212}{9}=0\Leftrightarrow9y^2+10y-212=0\)

Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có: