Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}

Ta luôn có \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) và \(\left|x-y\right|=\left|y-x\right|\)
\(\Rightarrow\left|x-2\right|=\left|2-x\right|;\left|x-4\right|=\left|4-x\right|;...;\left|x-8\right|=\left|8-x\right|;\left|x-10\right|=\left|10-x\right|\)
\(\Rightarrow A=\left|x-1\right|+\left|2-x\right|+\left|x+3\right|+\left|4-x\right|+...+\left|x-9\right|+\left|10-x\right|\)
\(\Rightarrow A\ge\left|x-1+2-x+x-3+4-x+...+x-9+10-x\right|\)
\(=\left|\left(x-x+x-x+x-x+...+x-x\right)+\left(2-1\right)+\left(4-3\right)+...+\left(10-9\right)\right|\)
\(=\left|0+1+1+1+1+1\right|\)
\(=5\)
\(\Rightarrow A\ge5\)
\(\Rightarrow\) GTNN của A = 5 tại \(\left(x-1\right)\left(2-x\right)\left(x-3\right)...\left(x-10\right)\ge0\)

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

11/Theo BĐT AM-GM,ta có; \(ab.\frac{1}{\left(a+c\right)+\left(b+c\right)}\le\frac{ab}{4}\left(\frac{1}{a+c}+\frac{1}{b+c}\right)\)\(=\frac{1}{4}\left(\frac{ab}{a+c}+\frac{ab}{b+c}\right)\)
Tương tự với hai BĐT kia,cộng theo vế và rút gọn ta được đpcm.
Dấu "=" xảy ra khi a= b=c
Ơ vãi,em đánh thiếu abc dưới mẫu,cô xóa giùm em bài kia ạ!
9/ \(VT=\frac{\Sigma\left(a+2\right)\left(b+2\right)}{\left(a+2\right)\left(b+2\right)\left(c+2\right)}\)
\(=\frac{ab+bc+ca+4\left(a+b+c\right)+12}{\left(ab+bc+ca\right)+4\left(a+b+c\right)+8+abc+\left(ab+bc+ca\right)}\)
\(\le\frac{ab+bc+ca+4\left(a+b+c\right)+12}{\left(ab+bc+ca\right)+4\left(a+b+c\right)+9+3\sqrt[3]{\left(abc\right)^2}}\)
\(=\frac{ab+bc+ca+4\left(a+b+c\right)+12}{ab+bc+ca+4\left(a+b+c\right)+12}=1\left(Q.E.D\right)\)
"=" <=> a = b = c = 1.
Mong là lần này không đánh thiếu (nãy tại cái tội đánh ẩu)

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:

 bit lm bài này k giup tui
bit lm bài này k giup tui
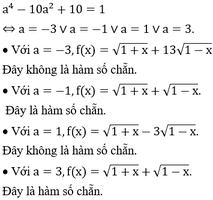
Đáp án B
A 7