Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt a=4453, b=1997
Ta có: \(F=5\dfrac{6}{a}\cdot\dfrac{1}{b}-\dfrac{2}{b}\cdot2\dfrac{3}{a}\)
\(=\dfrac{5a+6}{a}\cdot\dfrac{1}{b}-\dfrac{2}{b}\cdot\dfrac{2a+3}{a}\)+
\(=\dfrac{5a+6-4a-6}{ab}\)
\(=\dfrac{1}{b}\)
\(=\dfrac{1}{1997}\)

Đặt \(A=2\dfrac{1}{317}.\dfrac{3}{111}-\dfrac{316}{317}.\dfrac{1}{111}-\dfrac{4}{317.111}\)
\(=\left(2+\dfrac{1}{317}\right).\dfrac{3}{111}-\left(1-\dfrac{1}{317}\right).\dfrac{1}{111}-4.\dfrac{1}{317}.\dfrac{1}{111}\)
\(=6.\dfrac{1}{111}+3.\dfrac{1}{317}.\dfrac{1}{111}-\dfrac{1}{111}+\dfrac{1}{317}.\dfrac{1}{111}-4.\dfrac{1}{317}.\dfrac{1}{111}\)
Đặt \(a=\dfrac{1}{111};b=\dfrac{1}{317}\). Khi đó
\(A=6a+3ab-a+ab-4ab=5a=\dfrac{5}{111}\)
Vậy A=\(\dfrac{5}{111}\)

a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
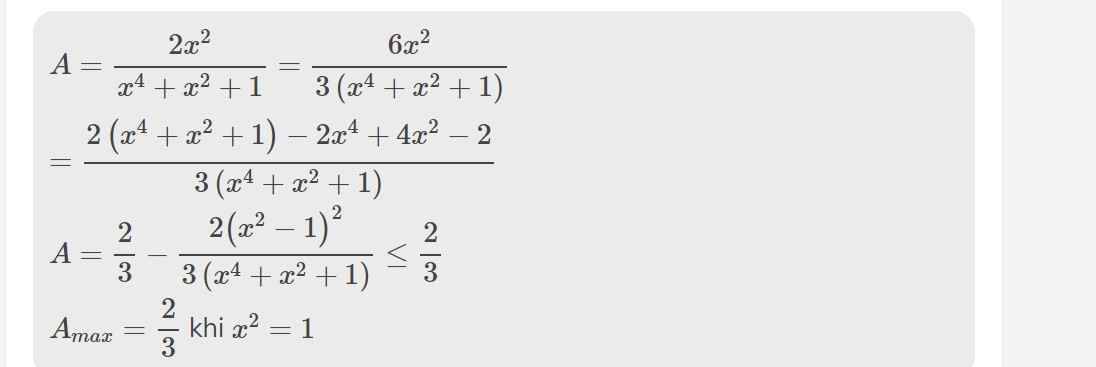

\(A=\left(\dfrac{x-1}{x\left(x-2\right)}+\dfrac{x+1}{x\left(x+2\right)}-\dfrac{4}{x\left(x-2\right)\left(x+2\right)}\right)\cdot\dfrac{x\left(x-3\right)}{2\left(x+2\right)}\)
\(=\dfrac{x^2+x-2+x^2-x+2-4}{x\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-3\right)}{2\left(x+2\right)}\)
\(=\dfrac{2x^2-4}{x\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-3\right)}{2\left(x+2\right)}\)
\(=\dfrac{2x\left(x^2-2\right)\left(x-3\right)}{2x\left(x-2\right)\cdot\left(x+2\right)^2}=\dfrac{\left(x^2-2\right)\left(x-3\right)}{\left(x-2\right)\left(x+2\right)^2}\)
Đặt 3179=a; 1111=b
\(K=2\dfrac{1}{a}\cdot\dfrac{3}{b}-\dfrac{a-1}{a}\cdot\dfrac{1}{b}-\dfrac{4}{a\cdot b}\)
\(=\dfrac{2a+1}{a}\cdot\dfrac{3}{b}-\dfrac{a-1}{ab}-\dfrac{4}{ab}\)
\(=\dfrac{6a+3-a+1-4}{ab}\)
\(=\dfrac{4a}{ab}=\dfrac{4}{b}=\dfrac{4}{1111}\)