Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

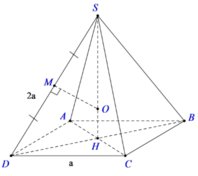
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC= OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có:

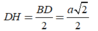
![]()
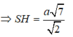
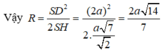

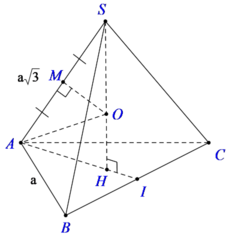
Gọi H là tâm của tam giác đều ABC.
Ta có SH ⊥ (ABC) nên SH là trục của tam giác ABC
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA (1)
Lại có, SH là trục của tam giác ABC và O ∈ SH nên: OA = OB = OC (2)
Từ (1) và (2) suy ra: OS = OA = OB = OC
Nên O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có 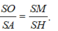
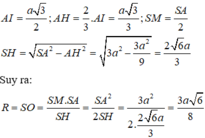

Gọi H trọng tâm của tam giác đều BCD.
Ta có AH ⊥ (BCD). Do đó
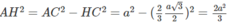
Vậy

Mặt khác OC 2 = OH 2 + HC 2
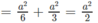
hay OC = OB = OD = (a 2 )/2
Vì BD = BC = CD = a nên các tam giác DOB, BOC, COD là những tam giác vuông cân tại O. Do đó hình chóp ODBC là hình chóp có đáy là tam giác đều nên tâm của mặt cầu ngoại tiếp phải nằm trên OH, ngoài ra tâm của mặt cầu ngoại tiếp này phải nằm trên trục của tam giác vuông DOB. Từ trung điểm C’ của cạnh BD ta vẽ đường thẳng song song với OC cắt đường thẳng OH tại I. Ta có I là tâm mặt cầu ngoại tiếp tứ diện OBCD. Mặt cầu này có bán kính là IC và IC 2 = IH 2 + HC 2
Chú ý rằng IH = OH/2 (vì HC′ = HC/2)
Do đó:
![]()


tại I. Ta có I là tâm mặt cầu ngoại tiếp tứ diện OBCD. Mặt cầu này có bán kính là IC và \(IC^2=\dfrac{1}{2}OH\) (vì \(HC'=\dfrac{1}{2}HC\))
Do đó :
\(IC^2=\dfrac{a^2}{24}+\dfrac{a^2}{3}=\dfrac{9a^2}{24}\)
hay \(IC=\dfrac{a\sqrt{6}}{4}\)

Gọi E là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AE\perp BC\\DE\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ADE\right)\)
Trong tam giác cân ADE (cân tại E), kẻ \(DH\perp AE\Rightarrow DH\perp\left(ABC\right)\)
\(\Rightarrow\widehat{DAE}=45^0\Rightarrow\Delta ADE\) vuông cân tại E
Gọi G và G' lần lượt là trọng tâm ABC và BCD. Trong mp (ADE), qua G kẻ đường thẳng d song song DE, qua G' kẻ d' song song AE. Gọi O là giao điểm d và d' \(\Rightarrow\) O là tâm mặt cầu ngoại tiếp tứ diện
Ta có: \(AE=DE=\dfrac{a\sqrt{3}}{2}\) ; \(AG=\dfrac{2}{3}AE=\dfrac{a\sqrt{3}}{3}\) ; \(OG=OG'=\dfrac{1}{3}AE=\dfrac{a\sqrt{3}}{6}\)
\(R=OA=\sqrt{AG^2+OG^2}=\dfrac{a\sqrt{15}}{6}\)
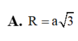
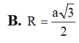
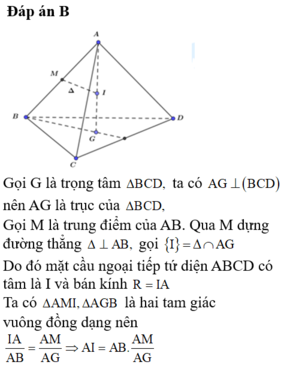

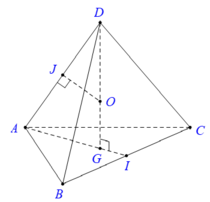

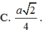
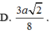
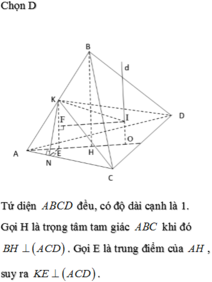

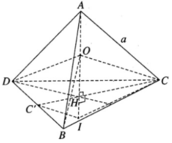
Gọi I là trung điểm cạnh BC, G là trọng tâm của tam giác ABC.
Trong mp (DAG), kẻ trung trực của DA cắt DG tại O thì: OD = OA = OB = OC nên O chính là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Bán kính R của mặt cầu bằng độ dài đoạn OD.
Trong tam giác ADG vuông tại G, ta có:
Mặt khác, tam giác DJO đồng dạng tam giác DGA nên:
Vậy bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a là R = a 6 4