
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m-2\right)\)
\(=4m^2-4m^2+4m+8\)
=4m+8
Để phương trình có hai nghiệm thì 4m+8>=0
hay m>=-2
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\left(-2m\right)^2-2\left(m^2-m-2\right)=4\)
\(\Leftrightarrow4m^2-2m^2+2m=0\)
=>2m(m+1)=0
=>m=0 hoặc m=-1

\(\Delta'=3-\left(-6\right)=9>0\)
vậy pt có 2 nghiệm pb
\(x_1=\sqrt{3}-3;x_2=\sqrt{3}+3\)

\(P=\dfrac{\sqrt{x}}{2\sqrt{x}-3}\)
\(\Leftrightarrow2P=\dfrac{2\sqrt{x}}{2\sqrt{x}-3}=1+\dfrac{3}{2\sqrt{x}-3}\)
Để \(P\in Z\) hay \(2P\in Z\) <=> \(\dfrac{3}{2\sqrt{x}-3}\in Z\)
Có \(x\in Z\)\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}\in Z^+\\\sqrt{x}\in I\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{x}-3\in Z\\2\sqrt{x}-3\in I\end{matrix}\right.\)
Trường hợp \(2\sqrt{x}-3\in I\) => \(\dfrac{3}{2\sqrt{x}-3}\notin Z\forall x\) thỏa mãn đk (L)
Trường hợp \(2\sqrt{x}-3\in Z\)
Để \(\dfrac{3}{2\sqrt{x}-3}\in Z\) <=> \(2\sqrt{x}-3\inƯ\left(3\right)=\left\{-1;1;-3;3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;2;0;3\right\}\) mà \(\sqrt{x}>0;\sqrt{x}\ne2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\)
Vậy...
(Kí hiệu I là số vô tỉ)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)


\(\widehat{ACD}=\widehat{BCD}-\widehat{BCA}=73-\left(90-\widehat{CBA}\right)=45\)=> Tam giác ACD vuông cân tại A=> AC=AD
Vẽ \(AH\perp DC\Rightarrow\hept{\begin{cases}AH//BE\\AH=DH=ACcos45=15\frac{\sqrt{2}}{2}sin62\end{cases}}\)
Xét \(AH//BE\Rightarrow\frac{EH}{DH}=\frac{AB}{AD}\Rightarrow\frac{EH}{AH}=\frac{AB}{AC}=cot62\Rightarrow EH=AHcot62=15\frac{\sqrt{2}}{2}sin62.cot62\)
\(=15\frac{\sqrt{2}}{2}cos62\)
Xét tam giác AHE vuông tại H \(\Rightarrow AE^2=AH^2+HE^2=\left(15\frac{\sqrt{2}}{2}\right)^2\left(sin^262+cos^262\right)=\left(15\frac{\sqrt{2}}{2}\right)^2\)
\(\Rightarrow AE=15\frac{\sqrt{2}}{2}cm\)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)


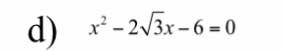



 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
4:
a: góc OAT+góc OMT=180 độ
=>OATM nội tiếp
b: Xét ΔAMC và ΔEOD có
góc MAC=góc OED
góc MCA=góc EDO
=>ΔAMC đồng dạng với ΔEOD