
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: \(\dfrac{a}{b}=\dfrac{5}{6}\)
=>\(\dfrac{a}{b}=\dfrac{5}{6}=\dfrac{a+5}{b+6}=\dfrac{a-5}{b-6}\)
=>\(\dfrac{a+5}{b+6}=\dfrac{a-5}{b-6}\)
=>\(\dfrac{a+5}{a-5}=\dfrac{b+6}{b-6}\)
Vậy nếu \(\dfrac{a+5}{a-5}=\dfrac{b+6}{b-6}\) thì\(\dfrac{a}{b}=\dfrac{5}{6}\).

a) \(1\dfrac{2}{3}-\left(\dfrac{1}{2}x-0,75\right)=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{5}{3}-\dfrac{1}{2}x+\dfrac{3}{4}=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{29}{12}-\dfrac{1}{2}x=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{2}x=\dfrac{29}{12}+\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{2}x=\dfrac{31}{12}\)
\(\Rightarrow x=\dfrac{31}{12}:\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{31}{6}\)
c) \(\left(x-1\dfrac{1}{2}\right)-\dfrac{3}{12}=\left(-\dfrac{1}{2}\right)^2\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)-\dfrac{3}{12}=\dfrac{1}{4}\)
\(\Rightarrow x-\dfrac{7}{4}=\dfrac{1}{4}\)
\(\Rightarrow x=\dfrac{1}{4}+\dfrac{7}{4}\)
\(\Rightarrow x=\dfrac{8}{4}\)
\(\Rightarrow x=2\)

\(=\dfrac{32}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\cdot\dfrac{-17}{3}=-\dfrac{9}{3}=-3\)
=(22/15.3/32) . (9/17 : -3/17)
=66/480 . (-3)
=11/80 . (-3)
=-33/80

\(\dfrac{8^{10}.15^{16}}{12^{15}.25^8}\)
\(=\dfrac{\left(2.4\right)^{10}.\left(3.5\right)^{16}}{\left(3.4\right)^{15}.\left(5^2\right)^8}\)
\(=\dfrac{2^{10}.4^{10}.3^{16}.5^{16}}{3^{15}.4^{15}.5^{16}}\)
\(=\dfrac{2^{10}.3}{4^5}\)
\(=\dfrac{2^{10}.3}{2^{10}}=3\)

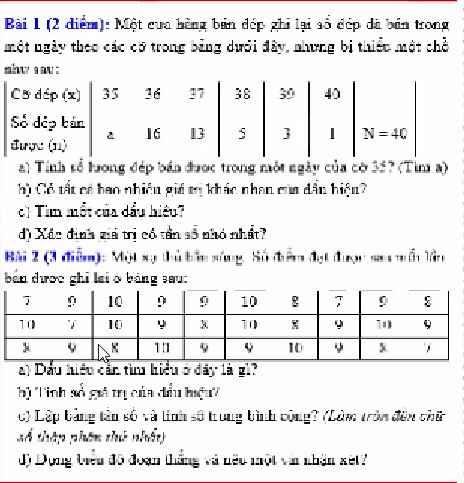
1 . a) dấu hiệu ở đây khối lượng của 20 học sinh lớp 7
-giá trị ở đây là 8
b)
| giá trị (x) | 30 32 33 34 35 36 38 46 |
| Tần số (n) | 2 3 1 2 1 6 4 1 N= 20 |
X= 30.2+32.3+33.1+34.2+35.1+ 36.6+ 38.4+46.1 : 20
= \(\dfrac{706}{20}\)=35,3

Câu trả lời của AN là sai bởi vì 21/56 rút gọn thành 3/8 và 3/8 viết được dưới dạng số thập phân hữu hạn bởi vì
8 khi phân tích ra thành thừa số nguyên tố chỉ chứa số 2, đồng nghĩa không chứa số nào khác 2 và 5
=>21/56 viết được dưới dạng số thập phân hữu hạn


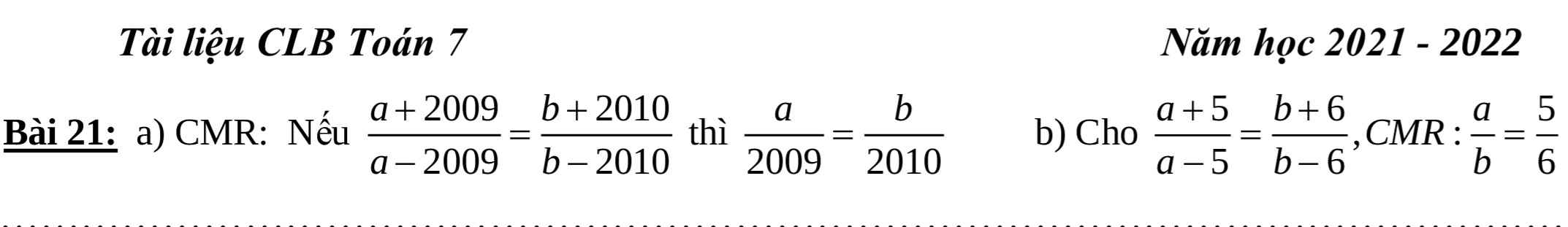
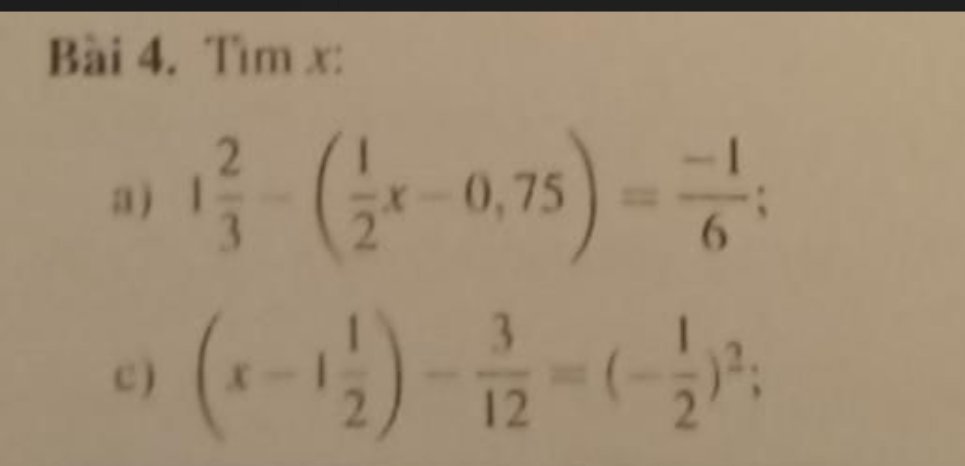

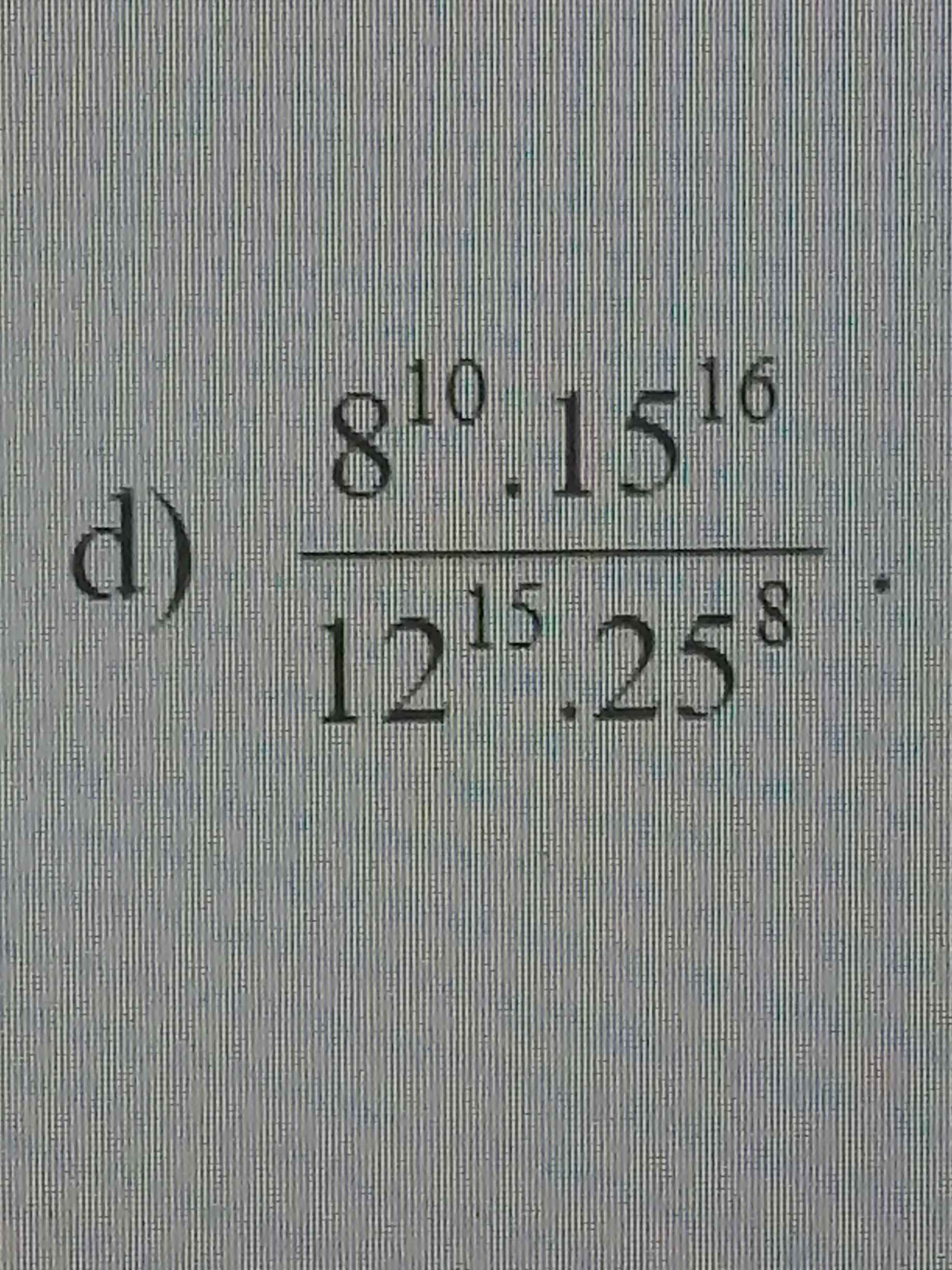

 nhanh giúp mình với ạ ,thông cảm hình hơi mờ
nhanh giúp mình với ạ ,thông cảm hình hơi mờ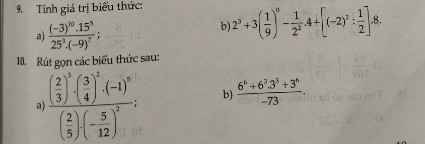
tự vẽ hình nha bạn
a.AC=\(\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8\) cm (pytago)
\(\Rightarrow\)chu vi tam giác ABC là: 6+10+8=24 cm
b.\(HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-AH^2}\left(pytago\right)\\ HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-AH^2}\left(pytago\right)\\ \Rightarrow HB< HC\)
okela