Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Áp dụng quy tắc nhân ta được số các số số tự nhiên có 3 chữ số và 3 chữ số đo đôi một khác nhau là: 9 x 9 x 8

Các chữ số được đặt trong các ô trống.
| . | . | . | . |
TH1: Số cần lập có chữ số 0:
Đưa 0 vào 3 cách
Đưa 1 vào 3 cách
Đưa 3 vào 2 cách
Lấy 1 số bất kì ô còn lại : 7 cách
=> TH1 có 126 số
TH2: Số cần lập không có chữ số 0:
Đưa 1 vào 4 cách
Đưa 3 vào 3 cách
Lấy 2 số bất kì đưa vào 2 ô còn lại : \(A^2_7\) cách
=> TH2 có 504 số
Vậy lập được tất cả 504 + 126 = 630 số

3:
Ta sẽ chia M ra làm 3 nhóm
Nhóm 1: \(A=\left\{0;3;6\right\}\)
Nhóm 2: \(B=\left\{1;4;7\right\}\)
Nhóm 3: \(C=\left\{2;5;8\right\}\)
TH1: 1 số A,1 số B, 1 số C
*Nếu số ở A chọn là số 0 thì sẽ có 3*3*2*2*1=36 cách
*Nếu số A chọn khác 0 thì sẽ là 2*3*3*3!=108 cách
=>Có 108+36=144 cách
TH2: 3 số A
=>Có 2*2*1=4 số
TH3: 3 số B
=>Có 3!=6 số
TH4: 3 số C
=>Có 3!=6 số
=>Có 144+4+6+6=148+12=160 số

Chọn B
Gọi số cần tìm thỏa mãn điều kiện bài toán là a b c d e f ¯ trong đó a,b,c,d,e,f ∈ S và đôi một khác nhau. Theo bài ra ta có
![]()
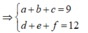
Có ![]()
![]() .
.
Ta có các cặp 3 số khác nhau từ S có tổng bằng 9 là ![]() .
.
![]()
![]()
![]()

Chọn B
Bước 1: ta xếp các số lẻ: có các số lẻ là 1,1,3,5 vậy có 5 ! 3 ! cách xếp.
Bước 2: ta xếp 3 số chẵn 2, 4, 6 xen kẽ 5 số lẻ trên có 6 vị trí để xếp 3 số vậy có A 6 3 cách xếp.
Vậy có 5 ! 3 ! A 6 3 = 2400 số thỏa mãn yêu cầu bài toán.



Gọi \(\overline{abc}\) là một số thỏa mãn yêu cầu bài toán
+) Nếu b = 0 thì a,c ∈ \(\left\{1;2;3;4;5;6;7;8;9\right\}\) ⇒ Chọn a,c có \(A_9^2\) cách
+) Nếu b = 1 thì a,c ∈ \(\left\{2;3;4;5;6;7;8;9\right\}\) ⇒ Chọn a,c có \(A_8^2\) cách
+) Nếu b = 2 thì a,c ∈ \(\left\{3;4;5;6;7;8;9\right\}\) ⇒ Chọn a,c có \(A_7^2\) cách
+) Nếu b = 3 thì a,c ∈ \(\left\{4;5;6;7;8;9\right\}\) ⇒ Chọn a,c có \(A_7^2\) cách
..............
+) Nếu b = 7 thì a,c ∈ \(\left\{8;9\right\}\) ⇒ Chọn a,c có \(A_2^2\) cách
* Nếu b = 8 thì a = c = 9 : không thỏa mãn yêu cầu bài toán
* Nếu b = 9 thì không có a,c
⇒ Số các số tự nhiên có 3 chữ số đôi một khác nhau sao cho chữ số hàng chục nhỏ hơn hai chữ số còn lại là
\(A_9^2\) + \(A_8^2\) + \(A_7^2\) + ... + \(A_2^2\)
= \(2.C_{10}^3\) = 240