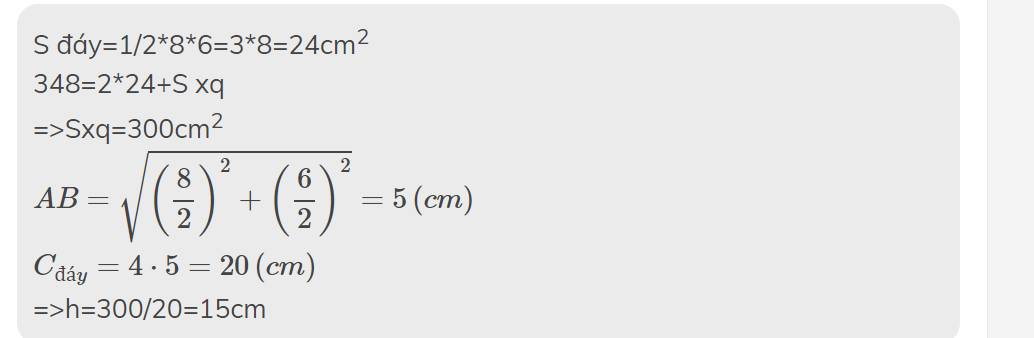Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

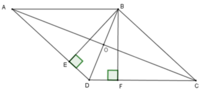
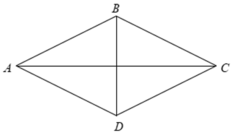
Gọi O là giao điểm của AC, BD.
Vì ABCD là hình thoi nên AC ⊥ BD; OA = OC = A C 2 = 40 cm; OB = OD = B D 2 = 30 cm.
Xét tam giác vuông AOB, theo định lý Pytago ta có:
AB2 = OA2 + OB2 = 402 + 302 = 2500 => 50 CM
Lại có: SABCD = A C . B D 2 = 60.80 2 = 2400 cm2 mà
SABCD = BE. AD ó BE.50 = 2400 ó BE = 48 cm (vì AD = AB = 50 cm)
Xét tam giác vuông BED có: ED2 = BD2 – BE2 = 602 – 482 = 1296 => ED = 36
Suy ra: SBED = 1 2 DE. BE = 1 2 .48.36 = 864 cm2.
Lại có: ΔBED = ΔBFD (ch – gn) nên SBFD = SBED = 864 cm2.
Từ đó: SBEDF = SBFD + SBED = 864 + 864 = 1728 cm2
Đáp án cần chọn là: D

Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :


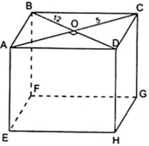
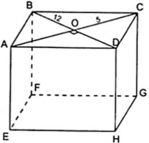
S đáy=1/2*8*6=3*8=24cm2
348=2*24+S xq
=>Sxq=300cm2
\(AB=\sqrt{\left(\dfrac{8}{2}\right)^2+\left(\dfrac{6}{2}\right)^2}=5\left(cm\right)\)
\(C_{đáy}=4\cdot5=20\left(cm\right)\)
=>h=300/20=15cm

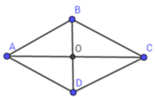
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B