Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
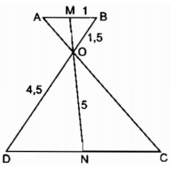
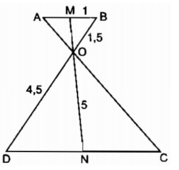
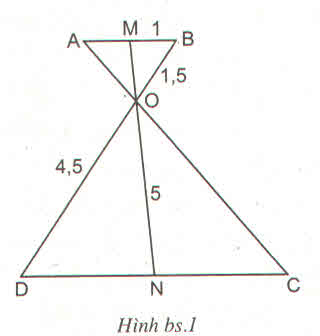
a)
\(\Delta OMB\approx\Delta OND\Rightarrow\dfrac{OB}{OD}=\dfrac{OM}{ON}\)
\(\left\{{}\begin{matrix}OM+ON=5\\\dfrac{OM}{ON}=\dfrac{1,5}{4,5}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}OM+ON=5\\3OM-ON=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}OM=\dfrac{5}{4}\left(cm\right)\\ON=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)
a) \(\dfrac{5}{4}=1,25\Rightarrow DA\left(A\right)\)
b) \(\dfrac{15}{4}=3+\dfrac{3}{4}=3,75\rightarrow PA\left(C\right)\)

Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)

cho tôi đoán mò nhé làA
nhé ủng hộ g=tôi bằng cách NHẤN ĐÚNG Ở DƯỚI
theo định lí ta lét trong tam giác ta có :
\(\dfrac{AB}{A`B`}=\dfrac{CD}{C`D`}\)=\(\dfrac{35}{105}=\dfrac{75}{C`D`}\)
=>C`D`=\(\dfrac{105.75}{35}\)=225
đáp án là C
Nguyễn Hà Anh nè ai cho bạn đoán mò chứ lập ra mà làm nhé
tick cho mình nha (sai thì hướng dẫn cho mình)

a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm




Chọn D