K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 5 2022
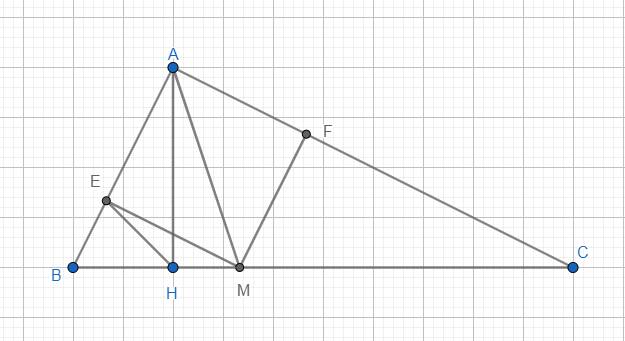
a) Xét △BEM và △BHA có:
\(\hat{B}\): chung
\(\hat{BEM}=\hat{BHA}\) = 90o
Do đó: △BEM đồng dạng △BHA (gg)
=> \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\) => BE.BA = BH.BM
b) Theo câu a), ta có:
BE.BA = BH.BM
=> \(\dfrac{BE}{BM}=\dfrac{BH}{BA}\)
Lại có: \(\hat{B}\): chung
nên △BEH đồng dạng △BMA (cgc)
=> \(\hat{BHE}=\hat{BAM}\)
Vì AM là tia phân giác của \(\hat{BAC}\) nên \(\hat{BAM}=\dfrac{\hat{BAC}}{2}=\dfrac{90^o}{2}=45^0\)
=> \(\hat{BHE}=45^0\)
mà \(\hat{BHA}=90^o\)
Nên HE là tia phân giác góc AHB.
1
1
KK
25 tháng 12 2016
Ta có \(a^2+b^2+c^2+ab+bc+ac\ge6\)
\(=>2\left(a^2+b^2+c^2+ab+bc+ac\right)\ge12\)
\(=>2a^2+2b^2+2c^2+2ab+2bc+2ac\ge12\)
\(=>a^2+b^2+c^2+a^2+b^2+c^2+2ab+2bc+2ac\ge12\)
Do \(a+b+c=3\)
\(=>\left(a+b+c\right)^2=9\\ =>a^2+b^2+c^2+2ab+2bc+2ac=9\)
Thế vào biểu thức \(a^2+b^2+c^2+a^2+b^2+c^2+2ab+2bc+2ac\ge12\)
Ta có \(a^2+b^2+c^2+9\ge12\)
\(=>a^2+b^2+c^2\ge3\) (1)
Ta có \(\begin{cases}a^2+b^2+c^2+2ab+2bc+2ac=9\\a^2+b^2+c^2+ab+bc+ac\ge6\end{cases}\)
\(=>\left(a^2+b^2+c^2+2ab+2bc+2ac\right)-\left(a^2+b^2+c^2+ab+ac+bc\right)\ge3\)
\(=>\left(2ab+2ac+2bc\right)-\left(ab+ac+bc\right)\ge3\)
\(=>ab+bc+ac\ge3\) (2)
Từ (1) và (2)
\(=>a^2+b^2+c^2+ab+bc+ac\ge6\)
16 tháng 6 2019
Tham khảo bài làm :
Câu hỏi của êfe - Toán lớp 7 - Học toán với OnlineMath
TB
7 tháng 6 2017
Áp dụng BĐT Cauchy Schwarz và BĐT \(a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\), ta có:
\(\left(2^2+2^2\right)\left[\left(a^2\right)^2+\left(b^2\right)^2\right]\ge\left(2a^2+2b^2\right)^2\)\(\ge\left[2\times\dfrac{1}{2}\left(a+b\right)^2\right]^2=\left(a+b\right)^4\)
\(\Leftrightarrow a^4+b^4\ge\dfrac{\left(a+b\right)^4}{8}\)
Dấu "=" xảy ra khi a = b
7 tháng 6 2017
Áp dụng BĐT Bunhiacopxki,ta có:
\(a^4+b^4\) \(\geq\) \(\dfrac{\left(a^2+b^2\right)^2}{2}\) \(\geq\) \(\dfrac{\left(\dfrac{1}{2}\left(a+b\right)^2\right)^2}{2}\) = \(\dfrac{\dfrac{1}{4}\left(a+b\right)^4}{2}\) = \(\dfrac{\left(a+b\right)^4}{8}\)
Dấu = xảy ra khi a=b
?