Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

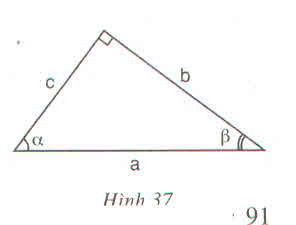
sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
a) b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC
b) b = c. (b/c) = c.tgB = c.cotgC
c = b.(c/b) = b.cotgB = b.tgC

sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC

- Giả sử tam giác ABC vuông tại A . Theo bài ra , ta có :
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\left(1\right)\)
- Áp dụng đlí Py - ta - go cho tam giác vuông ABC ( \(\widehat{A}=90^o\))
Ta có : \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow125^2=\left(\frac{3}{4}AC\right)^2+AC^2\)
\(\Leftrightarrow15625=\frac{9}{16}AC^2+AC^2\)
\(\Leftrightarrow15625=\left(\frac{9}{16}+1\right)AC^2\)
\(\Leftrightarrow\frac{25}{16}AC^2=15625\)
\(\Leftrightarrow AC^2=\frac{15625.16}{25}\)
\(\Leftrightarrow AC=\sqrt{\frac{15625.16}{25}}=\frac{125.4}{5}=100\left(cm\right)\)
Thay AC = 100cm vào (1) , ta được :
\(AB=\frac{3}{4}.100=75\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) đường cao AH , ta có :
\(AB^2=BH.BC\)
\(\Leftrightarrow BH=\frac{AB^2}{BC}=\frac{75^2}{125}=45\left(cm\right)\)
Ta lại có : BC = BH + HC
125 = 45 + HC
HC = 125 - 45 = 80 ( cm )
Vậy : AB = 75 cm
AC = 100 cm
HC = 80 cm
BH = 45 cm