Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
A:
20032003+1=20032002.2003+1=20032002+1
20032004+1=20032002.2003.2003+1=20032002.2003+1(loại số 2003 thứ hai của cả mẫu số và tử số)
B:
20032002+1=20032002+1
20032003+1=20032002.2003+1
Suy ra: A=B


Chọn B.
Số tập con gồm 2 phần tử của M và không chứa phần tử 1 là C 9 2 .

Ta có:
\(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{15}+\frac{1}{16}=\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\right)+\left(\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+\left(\frac{1}{9}+\frac{1}{10}+\frac{1}{11}\right)+\left(\frac{1}{12}+\frac{1}{13}+\frac{1}{14}\right)\)\(+\left(\frac{1}{15}+\frac{1}{16}\right)\)
Vì \(\frac{1}{6}+\frac{1}{7}+\frac{1}{8}<3.\frac{1}{6}=\frac{1}{2}\)
\(\frac{1}{9}+\frac{1}{10}+\frac{1}{11}<3.\frac{1}{9}=\frac{1}{3}\)
\(\frac{1}{12}+\frac{1}{13}+\frac{1}{14}<3.\frac{1}{12}=\frac{1}{4}\)
\(\frac{1}{15}+\frac{1}{16}<3.\frac{1}{15}=\frac{1}{5}\)
Nên \(A<2.\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\right)<2.\left(\frac{1}{2}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\right)=3\) (1)
Lập luận tương tự có:
A = ( 1/2 + 1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11 + 1/12) + (1/13 + 1/14 + 1/15 + 1/16) > (1/2 + 1/3 + 1/4) + 4 x 1/8 + 4 x 1/ 12 + 4 x 1/16
Hay A > 2 x (1/2 + 1/3 + 1/4) > 2 x (1/2 + 1/4 + 1/4) = 2 (2)
Từ (1) và (2) ta có 2 < A < 3. Vậy A không phải là số tự nhiên.
Có mình ra đề này rồi nhưng khác số và cũng giảng luôn. Mình ghi lời giải của mình ra rồi đưa vào đó làm được ko?
Đề của cô mình nè A=1/2+1/3+1/4+...+1/15+1/16.Chứng tỏ rằng A không phải là số tự nhiên.

Ta có
z = 1 + i 21 - 1 1 + i - 1 = 1 + i 21 - 1 i = 1 + i 2 10 1 + i - 1 i = - 2 10 + 2 10 + 1 i .
Vậy tổng phần thực và phần ảo của số phức z bằng 1
Đáp án A

Chọn ra 1 chẵn trong 5 chẵn và 1 lẻ trong 5 lẻ có số cách chọn bằng
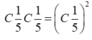
Chọn đáp án C.

ta có:
\(\frac{1}{19}>\frac{1}{40};\frac{1}{29}>\frac{1}{40};\frac{1}{31}>\frac{1}{40};\frac{1}{39}>\frac{1}{40}\)
\(\Rightarrow\frac{1}{19}+\frac{1}{29}+\frac{1}{31}+\frac{1}{39}>\frac{1}{40}.4\)=\(\frac{1}{10}\)