Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

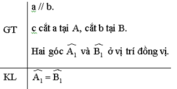
Chứng minh
Giả sử ∠(A1) ≠ ∠(B1)
Qua B kẻ đường thẳng xy sao cho ∠(ABy) = ∠(A1)
Mà hai góc này ở vị trí so le trong nên theo dấu hiệu của hai đường thẳng song song, ta có xy //a
+) Qua điểm B ta kẻ được hai đường thẳng b và xy cùng song song với đường thẳng a. Theo tiên đề Ơ- clit suy ra đường thẳng xy trùng với đường thẳng b.
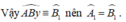
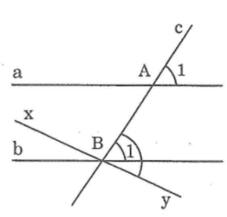

Cho 2 đường thẳng x và y song song với nhau
Đường thẳng d cắt x, y lần lượt tại A và B
Ta có x // y
=> \(\widehat{xAB}+\widehat{yBA}=180^o\) (Hai góc trong cùng phía)
Mà \(\widehat{yBA}+\widehat{yBd}=180^o\)(2 góc kề bù)
Nên \(\widehat{xAB}=\widehat{yBd}\)(đpcm)
Đây là 2 góc nằm ở vị trí đồng vị


đó là định lý vì tiên đề là qua 1 điểm ở ngoài dg thg ......
c/m: kẻ xy và zt và ff căt xy = A ;cắt zt =B ; theo gt có 1 cặp góc so le = nhau
lấy 1 diem C bất kỳ dựng 1 góc = góc so le tai A ......
Từ đó ta c/m ABCD là hình bình hành => xy // zt
( mk làm z đó, các bn cho ý kiến)

Ta có:
\(B_4=B_2\)(2 góc đối đỉnh)
\(B_4=A_2\)(2 góc so le trong)
\(\Rightarrow A_2=B_2\)
Ta có:
\(B_2=B_4\)(đối đỉnh)
\(B_2=A_4\)(so le trong)
\(\Rightarrow A_4=B_4\)
Ta có:
\(B_1=B_3\)(đối đỉnh)
\(B_3=A_1\)(so le trong)
\(\Rightarrow A_1=B_1\)
Ta có:
\(B_1=B_3\)(đối dỉnh)
\(B_1=A_3\)(so le trong)
\(\Rightarrow A_3=B_3\)
Ta Chứng minh được định lý:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì 2 góc đồng vị bằng nhau.
