Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đổi 15m/s = 54km/h.
Thời gian vật đi quãng đường thứ nhất là:
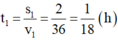
Thời gian vật đi quãng đường thứ hai là:
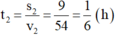
Thời gian vật đi quãng đường thứ ba là:
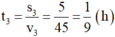
Áp dụng công thức ta có vận tốc trung bình của mô tô trên toàn bộ quãng đường là:
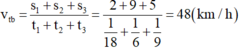

a, Gọi quãng đường từ A->C là x (x>=2,6(h))
Xét người 2: \(t_2=\dfrac{x}{5}+\dfrac{40-x}{15}\)
Xét người 1: \(t_1=\dfrac{x}{15}+\dfrac{40-x}{5}\)
t1 = t2 => x = 20(km) => AC = BC = 20*km)
b, \(v_{tb_1}=\dfrac{s_1+s_2}{t}=\dfrac{15+5}{2}=10\left(\dfrac{km}{h}\right)\)
\(v_{TB_2}=\dfrac{15+5}{2}=10\left(\dfrac{km}{h}\right)\)
c, Xe đạp không được xử dụng tron: \(t_o=\dfrac{x}{5}-\dfrac{x}{15}=\dfrac{20}{5}-\dfrac{20}{15}=2,7\left(h\right)\)

Chọn mốc thời gian tại 6h.
Chọn mốc quãng đường tại A.
Phương trình cho hai xe lần lượt là:
+Xe 1: s1=v1
+Xe 2: s2= v2t1 - v2ttrễ
Khi 2 xe gặp nhau ta có:
s1=s2
\(\Leftrightarrow\)v1t1= v2t1 - v2ttrễ
\(\Leftrightarrow\)v2ttrễ = v2t1 - v1t1 (Chuyển vế đổi dấu)
\(\Leftrightarrow\)v2ttrễ = t1(v2-v1) (Đặt nhân tử chung)
\(\Leftrightarrow\)t1=\(\dfrac{v_2t_{trễ}}{v_2-v_1}\) (Phương trình tìm x bình thường)
\(\Leftrightarrow\)t1=\(\dfrac{30}{30-18}\) (Vì ttrễ=1h nên mình hk thế số)
\(\Leftrightarrow\)t1=2,5 (h)
Vậy sau 2h30' nữa 2 xe gặp nhau
Vị trí gặp cách A là:
s1=v1t1
\(\Leftrightarrow\)s1=18*2,5=45km
tương tự ta có s2=sAB-s1=114-45=69km
Xong!

gọi s là nửa quãng đường => 2s là cả quãng đường
ta có : thời gian xe đi hết mỗi quãng đường là :
t1 = \(\dfrac{s}{v_1}\) = \(\dfrac{s}{35}\)
t2 = \(\dfrac{s}{v_2}\)
tổng thời gian xe đi hết quãng đường là :
t = t1 + t2 = \(\dfrac{s}{35}\) + \(\dfrac{s}{v_2}\) = \(\dfrac{s\left(v_2+35\right)}{35v_2}\)
ta có vận tốc trung bình của xe là :
vtb = \(\dfrac{2s}{\dfrac{s\left(v_2+35\right)}{35v_2}}\) = \(\dfrac{2s.35v_2}{s\left(35+v_2\right)}\) = \(\dfrac{70v_2}{35+v_2}\) = 40
=> 1400 + 40v2 = 70v2
=> 1400 = 30v2
=> v2 = 46,66667 (km/h)

bài 1
Gọi 2S la độ dài cả quãng đường
=> S là độ dài nửa quãng đường
Thời gian đi nửa quãng đầu là : \(\dfrac{S}{40}\left(h\right)\)
Thời gian đi 2/3 nửa quãng đường còn lại là : \(\dfrac{\dfrac{2}{3}.S}{50}=\dfrac{S}{75}\)
Thời gian đi 1/3 nửa quãng đường còn lại là : \(\dfrac{\dfrac{1}{3}S}{60}=\dfrac{S}{180}\left(h\right)\)
Vận tốc trung bình là :
\(v_{tb}=\dfrac{2S}{\dfrac{S}{40}+\dfrac{S}{75}+\dfrac{S}{180}}=\dfrac{2S}{\dfrac{79S}{1800}}\approx45,56\left(\dfrac{km}{h}\right)\)
Quãng đường đi được trong 1/4 thời gian t là
\(S_1=\dfrac{1}{4}.t.80=20t\left(km\right)\)
Quãng đường đi được trong 3/16 thời gian t là
\(S_2=\dfrac{3}{16}.t.60=11,25t\left(km\right)\)
Thời gian đi đoạn đường cuối cùng là
\(t-\dfrac{1}{4}.t-\dfrac{3}{16}t=\dfrac{9}{16}.t\left(h\right)\)
Quãng đường cuối cùng là
\(S_3=\dfrac{9}{16}.t.40=22,5t\left(km\right)\)
Vận tốc trung bình là
\(v_{tb}=\dfrac{20t+11,25t+22,5t}{t}=53,75\left(\dfrac{km}{h}\right)\)

\(20\)m/s=72km/h
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{60\cdot\dfrac{30}{60}+144}{\dfrac{30}{60}+\dfrac{144}{72}}=69,6\)km/h
1c; 2e ; 3d; 4a; 5b.