Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TXD: D=[-2;2].
Đặt:
t = x + 2 + 2 - x ( 2 ≤ t ≤ 2 2 ) ⇒ 2 4 - x 2 = 2 2 - x 2 + x = t 2 - 4
Khi đó hàm số trở thành:
y = f ( t ) = t 2 + t - 4 và có đạo hàm f ' ( t ) = 2 t + 1 > 0 trên D
=> hàm số đồng biến với mọi t ∈ [ 2 ; 2 2 ]
Do đó; min y = f(2)=2
m a x y = 4 + 2 2
Chọn A

Chọn C
Hàm số y =
x
2
+
x
+
4
x
+
1
là hàm phân thức có tập xác định là ![]() nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
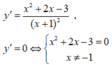
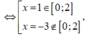
Ta có ![]()
=> A = 4, a = 3.
Vậy a + A = 7.

Chọn B
Xét f(x) = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có:
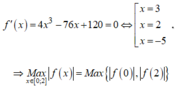
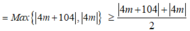
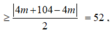
Dấu “=” xảy ra khi và chỉ khi ![]()
Nhận xét: Với trắc nghiệm thì ta thử đáp án được đáp án B

Chọn A
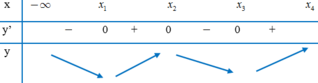
+ Hàm số trùng phương luôn đạt cực trị tại x = 0.
Do đó: x 1 , x 2 , x 3 = 0

Chọn B.
Ta có 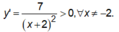
Do đó hàm số đồng biến trên [0;2].
Suy ra 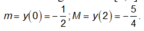
Do đó 4M – 2m = 6.


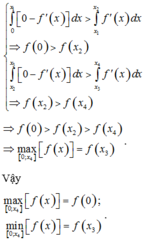
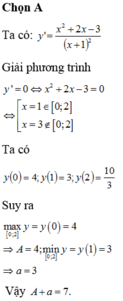




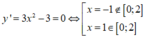
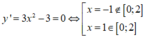
Đặt t= x4- 1( -1≤ t≤ 15).
Khi đó hàm số trở thành: y= ( t+1) 2+ t2+ 5=2t2+ 2t+6
Đạo hàm y’ = 4t+ 2> 0 mọi x thòa mãn 0≤ x≤ 2
Hàm số đồng biến trên đoạn [0; 2].
Hàm số đạt giá trị lớn nhất tại x= 2 tức là t= 15, hàm số đạt giá trị nhỏ nhất tại x= 0 hay t=1
Chọn D.