Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều dương là chiều chuyển động.
Góc thời gian lúc khởi hành
Ox trùng với quỹ đạo chuyển động.
O trùng với xe 1.
Ta có nếu đi cùng chiều sau 2h thì xe thứ 1 đuổi kịp xe 2 (t =2) thế vào : x1 = x2
<=> v1t = v2t
<=>2v1 = 2v2 + 40
<>v1=v2 + 40 (1)
Nếu 2xe đi ngược chiều 24 phút (t=0,4h) thì gặp nhau nên :
X1= x2
<=> v1t = 40 -v2t
<=> 0,4v1 = 40-0,4v2 (2)
Giải (1) và (2) : v1 =60
, v2 = 40.

mk làm ở bên hóa r` nhé
Câu hỏi của Đặng Yến Linh - Hóa học lớp 10 | Học trực tuyến

Giả sử hai xe gặp nhau ở C trong cả hai trường hợp cùng chiều và ngược chiều
Gọi v 12 là vận tốc của ô tô (1) đi từ A đối với ô tô (2) đi từ B
v 13 là vận tốc của ô tô (1) đi từ A đối với C
v 23 là vận tốc của ô tô (2) đi từ B đối với C
Khi hai ô tô chạy ngược chiều nhau thì v 13 và v 23 cùng phương ngược chiều nhau; v 12 và v 13 cùng phương cùng chiều nhau, còn v 23 ngược chiều với v 13 nên ta có
v 13 = v 12 – v 23
Suy ra: v 12 = v 13 + v 23
Hai ô tô cách nhau 1 đoạn đường s = 20km và chuyển động lại gần nhau và gặp nhau sau 15 phút. Do đó:
v 12 = s/t = 20/0,25 = 80km/h
Suy ra: v 13 + v 23 = 80 (1)
Khi hai ô tô cùng chiều thì cả ba vận tốc v ' 12 ; v 13 và v 23 cùng phương cùng chiều. Do đó
v 13 = v ' 12 + v 23
Suy ra: v ' 12 = v 13 – v 23
Hai ô tô gặp nhau sau 1h nên v ' 12 = s/t’ = 20/1 = 20km/h
Suy ra: v 13 – v 23 = 20 (2)
Từ (1), (2) ta suy ra hệ phương trình và giải hệ phương trình này ta được v 13 = 50km/h; v 23 = 30km/h

\(\Rightarrow\left\{{}\begin{matrix}0,5\left(v1+v2\right)=60\\2\left(v1-v2\right)=60\end{matrix}\right.\left(v1>v2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}v1+v2=120\\v1-v2=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v1=75\\v2=45\end{matrix}\right.\left(km/h\right)\)

15p = 1/4h; 30p = 1/2h
đi ngược chiều: (v1 + v2).1/4 = 20 (1)
đi cùng chiều: v1.1/2 -20 = v2.1/2 (2)
từ (1) và (2) có : \(\begin{cases}v_1+v_2=80\\v_1-v_2=40\end{cases}\)
đến đây trở thành bài toán: tổng-tỷ lop4 đã học giải ra:
v1 = 60km/h
v2 =20 km/h
ở đâu ra 1 ng vi diệu đến z, ta nói: 1 bài lop10 mà làm theo kiến thức lop7 nó nhẹ nhàng, dễ hiu quá đi thôi

Ta có:
- Thời gian hai xe gặp nhau khi đi ngược chiều: \(t_1=\)15 phút = \(\dfrac{1}{4}\left(h\right)\)
- Thời gian hai xe đuổi kịp nhau khi đi cùng chiều: \(t_2=1\left(h\right)\)
Do hai xe chuyển động ngược chiều nên:
\(v_3=v_1+v_2=\dfrac{s_{AB}}{t_1}=\dfrac{20}{\dfrac{1}{4}}=20\cdot4=80\left(km/h\right)\)
Nên: \(v_1+v_2=80\left(1\right)\)
Do hai xe chuyển động cùng chiều nên:
\(v_3'=v_1-v_2=\dfrac{s_{AB}}{t_2}=\dfrac{20}{1}=20\left(km/h\right)\)
Nên: \(v_1-v_2=20\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}v_1+v_2=80\\v_1-v_2=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_1+v_2=80\\2v_1=100\end{matrix}\right.\) (\(\left(v_1+v_1\right)-\left(v_2-v_2\right)=80+20\))
\(\Leftrightarrow\left\{{}\begin{matrix}v_1+v_2=80\\v_1=\dfrac{100}{2}=50\left(km/h\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}50+v_2=80\\v_1=50\left(km/h\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_2=30\left(km/h\right)\\v_1=50\left(km/h\right)\end{matrix}\right.\)
Nên giá trị của: \(2v_1+7v_2\) là:
\(2\cdot50-7\cdot30=100+210=310\left(km/h\right)\)
⇒ Chọn D

Chọn B.
Ta thấy v1 > v2. Độ lớn vận tốc của xe A so với xe B khi chạy ngược chiều và khi chạy cùng chiều lần lượt là:
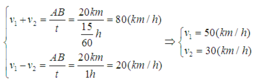
=> (3v1 + 7v2) = 360 (km/h).



Gọi v, v' là vận tốc 2 xe
30' = 0,5h
Tổng vận tốc 2 xe:
t = s/(v + v')
Hay 0,5 = 50/(v + v')
=> v + v' = 50/0,5 = 100 (1)
Hiệu vận tốc 2 xe:
t' = s/(v - v')
Hay 2 = 50/ (v - v')
=> v - v'= 50/2 = 25 (1)
Từ (1),(2) ta có:
v = (100 + 25) / 2 = 62,5 (km/h)
v' = 100 - 62,5 = 37,5 (km/h)
Vậy vận tốc 2 xe là 62,5km/h và 37,5km/h
\(s=50km\)
\(t_1=30'=\frac{1}{2}h\)
\(t_2=2h\)
v1= ?; v2 =?
GIẢI :
- chọn chiều dương là chiều chuyển động của mỗi xe. Quãng đường mỗi xe đi được trong khoảng thời gian là s=vt.
- Theo đề :
\(\left\{{}\begin{matrix}s_1+s_2=\left(v_1+v_2\right)t_1\Rightarrow\left(v_1+v_2\right).2=50\left(1\right)\\s_2-s_1=\left(v_2-v_1\right)t_1\Rightarrow\frac{v_2-v_1}{2}=50\left(2\right)\end{matrix}\right.\)
(1) => \(v_1+v_2=25\) => \(v_1=25-v_2\)
(2) => \(v_2-v_1=100\)
<=> \(v_2-25+v_2=100\)
<=> \(v_2=62,5\left(km/h\right)\)
=> \(v_1=25-62,5=-37,5\left(vôlí\right)\)