Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Từ phương trình : 64 x 1 2 + 36 x 2 2 = 48 2 c m (1) Thay x 1 = 3 cm, ta có:
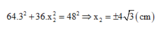
+ Đạo hàm phương trình (1), ta có:
![]()
⇒ 64 . 2 x 1 . x 1 ' + 36 . 2 x 2 . x 2 ' = 0 ⇒ 128 x 1 . x 1 ' + 72 x 2 . x 2 ' = 0
+ Theo định nghĩa vận tốc, ta có: v = x ' = ⇒ x 1 ' = v 1 x 2 ' = v 2
Thay vào phương trình trên ta có: 128 x 1 . v 1 + 72 x 2 . v 2 = 0 ⇒ v 2 = - 128 x 1 . v 1 72 x 2
+ Về độ lớn (tốc độ):
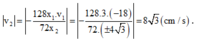

Đạo hàm: 64 x 1 2 + 32 x 2 2 = 48 2 (*)
→ 128 x 1 v 1 + 64 x 2 v 2 = 0 (**)
Tại thời điểm t: x 1 = 3cm, từ (*) → x 2 = 3 6 , theo (**) → x 2 = 6 6 cm/s.
Chọn C.

Ta có :
\(64^2_1x=36x^2_2=48^2\)
=> \(64x_1\le48^2\)
=> \(36x_2\le48^2\)
=> A1 = 6 (cm)
=> A2 = 8 (cm)
=> \(\frac{V_2}{V_1}=\frac{\omega\sqrt{A^2_2-x^2_2}}{\omega\sqrt{A^2_1-x^2_1}}=\frac{\sqrt{A^2_2-x^2_2}}{\sqrt{A^2_1-x^2_1}}=\frac{4}{3\sqrt{3}}\)
Vậy V2 = \(\frac{4.18}{3\sqrt{3}}=8\sqrt{3}\) (cm/giây)

Dùng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Suy ra hệ:
\(A^2=3^2+\dfrac{(8\pi)^2}{\omega^2}\)
\(A^2=4^2+\dfrac{(6\pi)^2}{\omega^2}\)
Từ đó tìm được:
\(A=5cm\)
\(\omega=2\pi(rad/s)\)
Ban đầu, vật qua VTCB theo chiều âm, suy ra \(\varphi=\dfrac{\pi}{2}(rad)\)
Vậy PT dao động: \(x=5\cos(2\pi t+\dfrac{\pi}{2})cm\)

Đáp án D
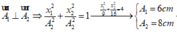
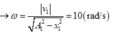
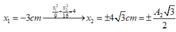
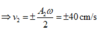
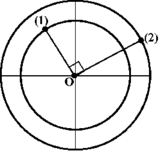 *Từ VTLG ta thấy chất điểm (1) và (2) chuyển động cùng chiều
*Từ VTLG ta thấy chất điểm (1) và (2) chuyển động cùng chiều
Nên độ lớn vận tốc tương đối của chúng là
![]()

Mỗi câu hỏi bạn nên hỏi 1 bài thôi nhé.
Bài 1:
Áp dụng công thức độc lập thời gian: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2= 2^2+\dfrac{(4\pi\sqrt 3)^2}{\omega^2}=3^2+\dfrac{(2\pi\sqrt 7)^2}{\omega^2}\)
\(\Rightarrow \omega=2\pi\) (rad/s)
Và \(A=4\) (cm)
Tìm pha ban đầu \(\varphi\) bằng cách: \(\cos(\varphi)=\dfrac{x_1}{A}=\dfrac{1}{2}\)
Ban đầu vật đi theo chiều dương \(\rightarrow \varphi <0\)
\(\Rightarrow \varphi=-\dfrac{\pi}{3}\)
Vậy PT: \(x=4\cos(2\pi t-\dfrac{\pi}{3})\) (cm)
b)
Biểu diễn dao động của vật bằng véc tơ quay như hình vẽ
Thời điểm đầu tiên vật qua x1 theo chiều âm ứng với véc tơ quay từ M đến N
Góc quay \(\alpha =60.2=120^0\)
Thời gian: \(i=\dfrac{120}{360}T=\dfrac{1}{3}s\)
Bài 2:
O chính là vị trí cân bằng với 2 biên là M, N
Thời gian vật đi từ O đến M là T/4
\(\Rightarrow T/4=6\Rightarrow T =24s\)
Biểu diễn dao động điều hoà bằng véc tơ quay ta có:
Vật đi từ O đến trung điểm I của ON ứng với véc tơ quay từ P đến Q
Góc quay: \(\alpha =30^0\)
Thời gian: \(t=\dfrac{30}{360}T=\dfrac{1}{12}.24=2(s)\)
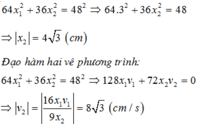
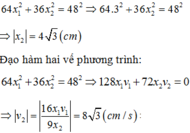


Chọn B
+ Thay x1 = 3cm vào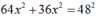 => x2 = ± 4cm.
=> x2 = ± 4cm.
+ Đạo hàm theo thời gian hai vế của phương trình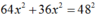 , ta được:
, ta được:
64. 2x1v1 + 36.2x2v2 = 0 (v chính là đạo hàm bậc nhất của x theo thời gian).
Hay 128.x1v1 + 72.x2v2 = 0. Thay giá trị của x1, x2 và v1 vào ta được |v2|= 24 cm/s.