Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Từ phương trình : 64 x 1 2 + 36 x 2 2 = 48 2 c m (1) Thay x 1 = 3 cm, ta có:
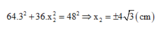
+ Đạo hàm phương trình (1), ta có:
![]()
⇒ 64 . 2 x 1 . x 1 ' + 36 . 2 x 2 . x 2 ' = 0 ⇒ 128 x 1 . x 1 ' + 72 x 2 . x 2 ' = 0
+ Theo định nghĩa vận tốc, ta có: v = x ' = ⇒ x 1 ' = v 1 x 2 ' = v 2
Thay vào phương trình trên ta có: 128 x 1 . v 1 + 72 x 2 . v 2 = 0 ⇒ v 2 = - 128 x 1 . v 1 72 x 2
+ Về độ lớn (tốc độ):
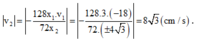

Chọn B
+ Thay x1 = 3cm vào ![]() => x2 = ± 4cm.
=> x2 = ± 4cm.
+ Đạo hàm theo thời gian hai vế của phương trình ![]() , ta được:
, ta được:
64. 2x1v1 + 36.2x2v2 = 0 (v chính là đạo hàm bậc nhất của x theo thời gian).
Hay 128.x1v1 + 72.x2v2 = 0. Thay giá trị của x1, x2 và v1 vào ta được |v2|= 24 cm/s.

Ta có :
\(64^2_1x=36x^2_2=48^2\)
=> \(64x_1\le48^2\)
=> \(36x_2\le48^2\)
=> A1 = 6 (cm)
=> A2 = 8 (cm)
=> \(\frac{V_2}{V_1}=\frac{\omega\sqrt{A^2_2-x^2_2}}{\omega\sqrt{A^2_1-x^2_1}}=\frac{\sqrt{A^2_2-x^2_2}}{\sqrt{A^2_1-x^2_1}}=\frac{4}{3\sqrt{3}}\)
Vậy V2 = \(\frac{4.18}{3\sqrt{3}}=8\sqrt{3}\) (cm/giây)

Chọn A
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.
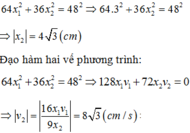
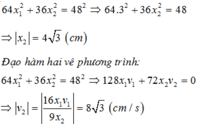



Đạo hàm: 64 x 1 2 + 32 x 2 2 = 48 2 (*)
→ 128 x 1 v 1 + 64 x 2 v 2 = 0 (**)
Tại thời điểm t: x 1 = 3cm, từ (*) → x 2 = 3 6 , theo (**) → x 2 = 6 6 cm/s.
Chọn C.