Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Chứng minh được B M ⏜ = M C ⏜ => AM là phân giác trong
Mặt khác: M A N ^ = 90 0
=> AN là phân giác ngoài

Bài 1
a/ Ta có : Góc AOK = góc xAC ( AC // OB )
Góc xAC = góc AEC ( góc tạo bởi t.t và dây cung và góc nt chắn cung AC )
Góc AEC = góc OEK ( 2 góc đối đỉnh )
=> góc AOK = góc OEK
Xét tam giác KOE và tam giác KAO ta có:
Góc OKE = góc OKA ( góc chung )
Góc OEK = góc AOK ( cmt )
=> tam giác KOE đồng dạng tam giác KAO (g-g)
=> \(\frac{KO}{KA}=\frac{KE}{KO}\)=>\(KO^2=KA.KE\)(1)
b/ Xét tam giác BEK và tam giác AKB ta có :
Góc EKB = góc AKB ( góc chung )
Góc EBK = góc BAK ( góc tạo bởi t.t và dây cung và góc nt chắn cung EB )
=> tam giác BEK đồng dạng tam giác ABK (g-g)
=> \(\frac{KE}{KB}=\frac{KB}{KA}\)=>\(KB^2=KE.KA\)(2)
(1) và (2) => \(KO^2=KB^2\)=>\(KO=KB\)=> K là trung điểm OB

à minh ghi thiếu, bài 2 là người ta giao cho tổ A làm trong một thời gian nhất định

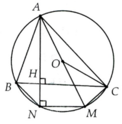
a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân

Pt 1: 4(1/a + 1/b )= 1
Pt 2: 1/a + 3/b = 5/12
Từ 2 pt ta được hpt sau đó giải a,b với a là t/g người t1 làm cv đó, b là t/g người t2 làm cv đó

a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
hay \(\widehat{ACM}=90^0\)
b: \(\widehat{OAC}+\widehat{AMC}=90^0\)
\(\widehat{BAH}+\widehat{ABC}=90^0\)
mà \(\widehat{AMC}=\widehat{ABC}\)
nên \(\widehat{OAC}=\widehat{BAH}=\widehat{OCA}\)
Xét \(\Delta OAC\) có : \(OA=OC\left(=R\right)\left(gt\right)\)
\(\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OAC}=\widehat{ACO\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow\widehat{BAH=\widehat{OCA}}\)
c) Xét \(\left(O\right)\), có : \(\widehat{ANM=90^0}\)
\(\Rightarrow MN\pm AN\)
\(MàBC\pm AN\left(gt\right)\)
\(\Rightarrow MN=BC\)
Xét tam giác \(BNMC\)\(cóMN=BC\left(cmt\right)\)
Tam giác BNMC là hình thang
Mà bốn đỉnh B,M,N,C
Vậy BMNC là tam giác cân

a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
b: \(\widehat{BAH}+\widehat{ABC}=90^0\)
\(\widehat{OAC}+\widehat{AMC}=90^0\)
mà \(\widehat{ABC}=\widehat{AMC}\left(=\dfrac{sđ\stackrel\frown{AC}}{2}\right)\)
nên \(\widehat{BAH}=\widehat{OAC}=\widehat{OCA}\)