Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian mỗi đội làm một mình để xong công việc lần lượt là \(x,y\left(h\right);x,y>0\).
Mỗi giờ mỗi đội làm được lần lượt số phần công việc là: \(\frac{1}{x},\frac{1}{y}\)công việc.
Theo bài ra ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\3\left(\frac{1}{x}+\frac{1}{y}\right)+\frac{3}{y}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{6}\\\frac{1}{y}=\frac{1}{12}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=12\end{cases}}\left(tm\right)\).

Giả sử nếu làm riêng thì người thứ nhất hoàn thành công việc trong x giờ, người thứ hai trong y giờ. Điều kiện x > 0, y > 0.
Trong 1 giờ người thứ nhất làm được 1/x công việc, người thứ hai 1/y công việc, cả hai người cùng làm chung thì được 1/8 công việc.
Ta được : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\)
Trong 3 giờ, người thứ nhất làm được 3/x công việc, trong 4 giờ người thứ hai làm được 4/y công việc, cả hai người làm được 4/5 công việc
Ta được\(\frac{3}{x}+\frac{4}{x}=\frac{4}{5}\)
Ta có hệ phương trình : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\\\frac{3}{x}+\frac{4}{x}=\frac{5}{4}\end{cases}}\)
Giải ra ta được x = \(\frac{35}{4}\), y = \(\frac{280}{3}\)
Vậy người thứ nhất 35/4 giờ, người thứ hai 280/3 giờ.

đổi 2 giờ 40 phút=\(\dfrac{8}{3}\) giờ
gọi thời gian đội 1 và đội 2 làm riêng để hoàn thành công việc lần lượt là
x,y(x,y>\(\dfrac{8}{3}\) )
=>hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{\dfrac{8}{3}}=\dfrac{3}{8}\\y-x=4\end{matrix}\right.\) giải hệ pt trên ta được \(\left\{{}\begin{matrix}x=4\left(TM\right)\\y=8\left(TM\right)\end{matrix}\right.\)
vậy nếu làm riêng để hoàn thành công việc thì đội thứ nhất hết 4 giờ
đội thứ 2 hết 8 giờ

TK:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒
15
×
y
+
15
×
y
=
1
(
1
)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒
3
×
x
+
5
×
y
=
1
4
⇒
5
×
(
3
×
x
+
5
×
y
)
=
5
×
1
4
15
×
x
+
25
×
y
=
5
4
(
2
)
Lấy (2) trừ đi (1) ta được:
(
15
×
x
+
25
×
y
)
−
(
15
×
x
+
15
×
y
)
=
5
4
−
1
10
×
y
=
1
4
y
=
1
4
:
10
⇒
y
=
1
40
⇒
x
=
1
24
Vậy .................
Tham Khảo:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒15×y+15×y=1(1)⇒15×y+15×y=1(1)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒3×x+5×y=14⇒3×x+5×y=14
⇒5×(3×x+5×y)=5×14⇒5×(3×x+5×y)=5×14
15×x+25×y=54(2)15×x+25×y=54(2)
Lấy (2) trừ đi (1) ta được:
(15×x+25×y)−(15×x+15×y)=54−1(15×x+25×y)−(15×x+15×y)=54−1
10×y=1410×y=14
y=14:10y=14:10
⇒y=140⇒y=140
⇒x=124⇒x=124
Vậy .................

Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
\(\Rightarrow15\times y+15\times y=1\left(1\right)\)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
\(\Rightarrow3\times x+5\times y=\frac{1}{4}\)
\(\Rightarrow5\times\left(3\times x+5\times y\right)=5\times\frac{1}{4}\)
\(15\times x+25\times y=\frac{5}{4}\left(2\right)\)
Lấy (2) trừ đi (1) ta được:
\(\left(15\times x+25\times y\right)-\left(15\times x+15\times y\right)=\frac{5}{4}-1\)
\(10\times y=\frac{1}{4}\)
\(y=\frac{1}{4}:10\)
\(\Rightarrow y=\frac{1}{40}\)
\(\Rightarrow x=\frac{1}{24}\)
Vậy .................
Chúc bạn học tốt

Gọi x,y(h) lần lượt thời gian làm riêng xong cv của người 1 và 2(x,y>0)
Trong 1h người 1 làm được 1/x công việc
Trong 1h người 2 làm được 1/y công việc
Trong 1h 2 người làm chung được 1/16 công việc
Ta có pt1: 1/x + 1/y = 1/16
Trong 3h người 1 làm được 3/x công việc
Trong 6h người 2 làm được 6/y công việc
Ta có pt2: 3/x + 6/y =1/4
DONE
Hệ bạn tự giải nha

Gọi x (giờ) là thời gian đội I làm một mình xong công việc (x > 12)
Thời gian đội thứ II làm một mình xong công việc là: x – 7 (giờ)
Trong một giờ đội I làm được 1/x (công việc)
Trong một giờ đội II làm được 1/(x-7) (công việc)
Trong một giờ cả hai đội làm được 1/12 (công việc)
Theo bài ra ta có phương trình:
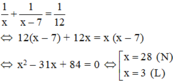
Vậy thời gian đội I làm xong công việc là 28 giờ, thời gian đội II làm xong công việc là: 28 – 7 = 21 (giờ)
Đáp án: C
Gọi \(x\left(giờ\right),y\left(giờ\right)\) lần lượt là thời gian của đội thứ nhất và đội thứ hai làm riêng xong công việc (x, y > 0)
Trong một giờ hai đội làm được: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\) (công việc)
Đội thứ nhất làm trong 3 giờ rồi đội thứ hai làm tiếp trong 4 giờ được 0,8 công việc nên ta có:
\(\dfrac{3}{x}+\dfrac{4}{y}=0,8\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{3}{x}+\dfrac{4}{y}=0,8\end{matrix}\right.\)
Đặt \(u=\dfrac{1}{x};v=\dfrac{1}{y}\), ta có:
\(\left\{{}\begin{matrix}u+v=\dfrac{1}{4}\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4.\dfrac{1}{5}+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v=\dfrac{1}{20}\\u=\dfrac{1}{5}\end{matrix}\right.\)
*) \(u=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{5}\Leftrightarrow x=5\) (nhận)
*) \(v=\dfrac{1}{20}\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{20}\Rightarrow y=20\) (nhận)
Vậy đội thứ nhất làm riêng trong 5 giờ xong công việc
đội thứ hai làm riêng trong 20 giờ xong công việc