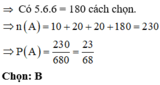Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .

Đáp án A
Gọi số cần tìm có dạng a b c d ¯ vì a b c d ¯ chia hết cho 6 ⇒ d = { 2 ; 4 ; 6 ; 8 } a + b + c + d : 3 .
Khi đó, chọn d có 4 cách chọn; b và c đều có 9 cách chọn (từ 1 → 9 )
Nếu b + c + d:3 thì a = {3;6;9} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 1 thì a = {2;5;8} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 2 thì a = {1;4;7} ⇒ có 3 cách chọn a
Suy ra a chỉ có 3 cách chọn ⇒ có 4.9.9.3 = 972 số chia hết cho 6
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .

Đáp án A.
Gọi số cần tìm có dạng
a
b
c
d
vì chia hết cho 6 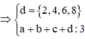
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1→9).
· Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là ![]()

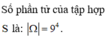
Gọi là biến cố: Chọn được 1 số chia hết cho 6 từ tập hợp S”
Số chia hết cho 6 có dạng: 


Tập S có 9 4 phần tử. Ta có
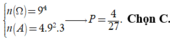
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
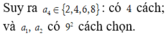
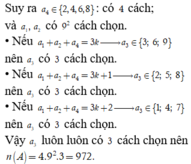

Phương pháp:
Công thức tính xác suất của biên cố A là: P A = n A n Ω

Gọi A là biến cố: “Chọn ngẫu nhiên 3 phần tử của tập S sao cho tổng của 3 phần tử chia hết cho 3”.
Trong tập hợp S có 5 số chia hết cho 3 là


TH4: Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2