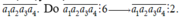Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi mẫu là x
Theo đề, ta có:
\(\dfrac{2}{5}< \dfrac{4}{x}< \dfrac{2}{3}\)
=>10>x>6
=>\(x\in\left\{9;8;7\right\}\)
b: Phần phân số là 1-9/25=16/25
Phần nguyên là 125x9/25=45
Vậy: Hỗn số cần tìm là \(45\dfrac{16}{25}\)

a) \(\frac{1}{n}\) - \(\frac{1}{n+1}\) = \(\frac{n+1}{n\left(n+1\right)}\) - \(\frac{n}{n\left(n+1\right)}\) = \(\frac{1}{n\left(n+1\right)}\) = \(\frac{1}{n}\) . \(\frac{1}{n+1}\) =>đpcm
b) A= \(\frac{1}{2}\) - \(\frac{1}{3}\) + \(\frac{1}{3}\) - \(\frac{1}{4}\)+...+\(\frac{1}{8}\) - \(\frac{1}{9}\) +\(\frac{1}{9}\)
= \(\frac{1}{2}\) + \(\frac{1}{9}\)= \(\frac{11}{18}\)

c1 chắc có lộn đề r
c2:Gọi 2 số cần tìm lần lượt là a,b
Ta có: 9/11a=6/7b
a+b=258 nên a=258-b
=>9/11*(258-b)=6/7b
2322/11-9/11b=6/7b
6/7b+9/11b=2322/11
66/77+63/77b=2322/11
129/77b=2322/11
b=2322/11:129/77=126
nên a=258-126=132
Vậy 2 số cần tìm lần lượt là 132;126

a: \(B=\left(-\dfrac{1}{5}-\dfrac{5}{7}+\dfrac{-3}{35}\right)+\left(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{2}\right)+\dfrac{1}{41}\)
\(=\dfrac{-7-25-3}{35}+\dfrac{3+2+1}{6}+\dfrac{1}{41}=\dfrac{42}{41}-1=\dfrac{1}{41}\)

Bạn xem cách điền của mình nhé:
Giải:
Phép chia 5 cho 7 được viết là: \(5:7\)
Phép chia 1,7 cho 3,12 được viết là: \(1,7:3,12\)
Phép chia 15cho 34 được viết là: \(\frac{1}{5}:\frac{3}{4}\)
Phép chia −314cho 5 được viết là: \(-3\frac{1}{4}:5\)
Phép chia số a cho số b (b ≠≠0) được viết là: \(a:b\) (hoặc \(\frac{a}{b}\))
Chúc bạn học tốt!![]()
Phép chia 5 cho 7 được viết là\(\frac{5}{7}\)
Phép chia 1,7 cho 3,12 được viết là:1,7:3,12
Phép chia \(\frac{1}{5}\) cho \(\frac{3}{4}\) được viết là:\(\frac{1}{5}:\frac{3}{4}\)
Phép chia \(-\frac{1}{4}\) cho 5 được viết là:\(-3\frac{1}{4}\):5
Phép chia số a cho số b (b ≠0) được viết là:a:b(\(\frac{a}{b}\))

bài 2 ta giải cách khác
Theo đề bài , ta gọi a là số An nghĩ . Ta có :
a-8 chia hết cho 7 => a-1 chia hết cho 7 (1)
a-9 chia hết cho 8 => a-1 chia hết cho 8 (2)
a-10 chia hết cho 9=> a-1 chia hết cho 9(3)
Từ (1) ; (2); (3), ta có a-1 là BC(7 ; 8 ; 9)
Ta có :
7 = 1 x 7
8 = 23
9 = 32
=> BCNN(7 ; 8 ; 9)= 7 x 23 x 32= 504
=> a-1thuộc B(504)= { 0;504;1008;.........................}
=> a thuộc { 1;505;1009;....................................}
Mà a là số có 3 chữ số
=> a = 505
Kết luận : Vậy số mà bạn An nghĩ ra là số 505
gọi số phải tìm là n
ta có:
n = 7.k + 8 = 7(k+1) +1
n = 8.m + 9= 8(m+1) +1
n = 9.p +10 = 9(p+1) +1
* từ đó thấy rằng số n là bội số chung của 7,8,9 +1
vậy số nhỏ nhất n= 7.8.9 +1 = 505
vì n là số có 3 chữ số n=505 là duy nhất
* thử lại:
(505-8)/7= 71
(505-9)/8= 62
(505-10)/9=55
Tập S có 9 4 phần tử. Ta có
Thật vậy: Gọi số thỏa mãn biến cố là