Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Có : ^BCK = ^BAK ( chắn cung BK )
^BAK = ^BCH (Phụ ^ABC)
=> ^HCA1 = ^A1CK
=> CA1 là phân giác ^HCK
Tam giác HCK có CA1 vừa là đường cao vừa là phân giác
=> \(\Delta\)HCK cân tại C
=> CA1 là trung tuyến
=> A1 là trung điểm HK
b,\(\frac{HA}{AA_1}+\frac{HB}{BB_1}+\frac{HC}{CC_1}=1-\frac{HA_1}{AA_1}+1-\frac{HB_1}{BB_1}+1-\frac{HC_1}{CC_1}\)
\(=3-\frac{S_{BHC}}{S_{ABC}}-\frac{S_{AHC}}{S_{ABC}}-\frac{S_{AHB}}{S_{ABC}}\)
\(=3-1\)
\(=2\)
c,D \(OM\perp BC\)tại M nên M là trung điểm BC
Xét \(\Delta\)BB1C vuông tại B1 có B1M là trung tuyến
=> B1M = MB = MC
=> ^MBB1 = ^MB1B
và ^MB1C = ^MCB1
Mà ^B1AE = ^B1BC (Chắn cung EC)
^MB1C = ^AB1N (đối đỉnh)
^BB1M + ^CB1M = 90o
=> ^NAB1 + ^NB1A = 90o
=> \(B_1N\perp AE\)
Theo hệ thức lượng trong tam giác vuông có:
\(AB_1^2=AN.AE\)
\(EB_1^2=EN.EA\)
\(\Rightarrow\frac{AB_1^2}{EB_1^2}=\frac{AN.AE}{EN.EA}=\frac{AN}{EN}\)

Gọi D, E, F lần lượt là chân đường cao hạ từ A, B, C của tam giác ABC.
+) \(\Delta AHE~\Delta ACD\)( vì ^HAE =^CAD, ^HEA=^CDA )
=> \(\frac{HA}{CA}=\frac{EA}{AD}\)=> \(\frac{HA}{CA}.\frac{HB}{BC}=\frac{EA}{CA}.\frac{HB}{BC}=\frac{2.EA.HB}{2.CA.BC}=\frac{S_{\Delta AHB}}{S_{ABC}}\)(1)
+) \(\Delta CHD~\Delta CBF\)( vì ^DCH=^FCB, ^CDH=^CFB )
=> \(\frac{CH}{CB}=\frac{CD}{CF}\)=> \(\frac{CH}{CB}.\frac{AH}{AB}=\frac{CD.AH}{CF.AB}=\frac{S_{AHC}}{S_{ABC}}\)(2)
+) \(\Delta ABE~\Delta HBF\)
=> \(\frac{HB}{AB}=\frac{BF}{BE}\Rightarrow\frac{HB}{AB}.\frac{HC}{AC}=\frac{BF.HC}{BE.AC}=\frac{S_{BHC}}{S_{ABC}}\)(3)
Từ (1) ; (2) ; (3) => \(\frac{HA}{CA}.\frac{HB}{BC}+\frac{CH}{CB}.\frac{AH}{AB}+\frac{HB}{AB}.\frac{HC}{AC}=\frac{S_{ABE}}{S_{ABC}}+\frac{S_{ABE}}{S_{ABC}}+\frac{S_{ABE}}{S_{ABC}}=1\)
=> \(\frac{HA}{BC}.\frac{HB}{AC}+\frac{HB}{AC}.\frac{HC}{AB}+\frac{HC}{AB}.\frac{HA}{BC}=1\)
Đặt: \(\frac{HA}{BC}=x;\frac{HB}{AC}=y;\frac{HC}{AB}=z\); x, y, z>0
Ta có: \(xy+yz+zx=1\)
=> \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)=3\)
=> \(x+y+z\ge\sqrt{3}\)
"=" xảy ra khi và chỉ khi x=y=z
Vậy : \(\frac{HA}{BC}+\frac{HB}{AC}+\frac{HC}{AB}\ge\sqrt{3}\)
"=" xảy ra <=> \(\frac{HA}{BC}=\frac{HB}{AC}=\frac{HC}{AB}\)

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{HB}{HC}\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(BD\cdot BA=BH^2\)
\(\Leftrightarrow BD=\dfrac{HB^2}{AB}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(CE\cdot CA=CH^2\)
\(\Leftrightarrow EC=\dfrac{HC^2}{AC}\)
Ta có: \(\dfrac{BD}{EC}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\dfrac{HB^2}{AB}\cdot\dfrac{AC}{HC^2}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\left(\dfrac{HB}{HC}\right)^2\cdot\dfrac{AC}{AB}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\left(\dfrac{AB}{AC}\right)^4\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)(đpcm)
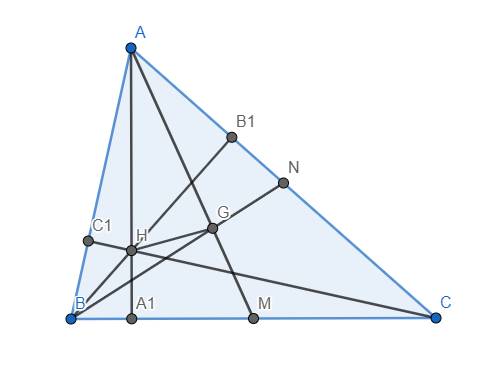
Đặt AA1 = a , BB1 = b , CC1 = c , HA1 = x , HB1 = y , HC1 = z (với a,b,c,x,y,z > 0)
a) Đầu tiên , ta cần chứng minh : \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) .
Thật vậy : \(\frac{x}{a}=\frac{x.BC}{a.BC}=\frac{S_{HBC}}{S_{ABC}}\); \(\frac{y}{b}=\frac{y.AC}{b.AC}=\frac{S_{AHC}}{S_{ABC}}\); \(\frac{z}{c}=\frac{z.AB}{c.AB}=\frac{S_{ABH}}{S_{ABC}}\)
\(\Rightarrow\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Ta có : \(\frac{AA_1}{HA_1}+\frac{BB_1}{HB_1}+\frac{CC_1}{HC_1}=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).1=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)\)
\(\ge\left(1+1+1\right)^2=9\)(áp dụng bđt Bunhiacopxki)
Vậy ta có đpcm
b) Ta có : \(\frac{HA_1}{HA}+\frac{HB_1}{HB}+\frac{HC_1}{HC}=\frac{x}{a-x}+\frac{y}{b-y}+\frac{z}{c-z}=\frac{1}{\frac{a}{x}-1}+\frac{1}{\frac{b}{y}-1}+\frac{1}{\frac{c}{z}-1}\)
Áp dụng bđt \(\frac{m^2}{i}+\frac{n^2}{j}+\frac{p^2}{k}\ge\frac{\left(m+n+p\right)^2}{i+j+k}\)(bạn tự chứng minh)
Ta có : \(\frac{1^2}{\frac{a}{x}-1}+\frac{1^2}{\frac{b}{y}-1}+\frac{1^2}{\frac{c}{z}-1}\ge\frac{\left(1+1+1\right)^2}{\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)-3}\ge\frac{9}{9-3}=\frac{3}{2}\)
(Từ câu a. ta có \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\ge9\))
Vậy ta có đpcm
Đúng hay sai:
\(\frac{\sqrt{a^2+b^2}}{\sqrt{59+2}}=\frac{\sqrt{89^{x3+8}}}{\sqrt[46]{78+1}}\)
x O v" O