Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(d:\) \(y=ax+b\Rightarrow1=a.+b\Rightarrow b=1-a\Rightarrow y=ax+1-a\) (a<0)
\(\Rightarrow A\left(\frac{a-1}{a};0\right)\); \(B\left(0;1-a\right)\)
Khi quay OAB quanh Oy sẽ thu được khối nón tròn xoay có bán kính đáy \(R=\left|y_B\right|=\left|1-a\right|=1-a\), chiều cao \(h=\left|x_A\right|=\left|\frac{a-1}{a}\right|=\frac{a-1}{a}\)
Thể tích nón: \(V=\frac{1}{3}\pi R^2h=\frac{1}{3}\pi\left(1-a\right)^2.\frac{\left(a-1\right)}{a}=\frac{\pi\left(a-1\right)^3}{3a}\)
Xét hàm \(f\left(a\right)=\frac{\left(a-1\right)^3}{a}\Rightarrow f'\left(a\right)=\frac{2a^3-3a^2+1}{a^2}=\frac{\left(2a+1\right)\left(a-1\right)^2}{a^2}\) (\(a< 0\))
\(f\left(a\right)\) đạt cực tiểu tại \(a=-\frac{1}{2}\Rightarrow V_{min}=V\left(\frac{1}{2}\right)=\frac{9\pi}{4}\)

Đáp án: D.
Hướng dẫn: Thể tích khối tròn xoay này được tính bởi
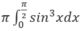

Chọn đáp án D.
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
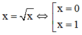
Thể tích cần tính:
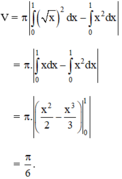

Đáp án: D.
Vì thể tích khối này được tính bởi
![]()
như vậy A và C dễ thấy là sai.

Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là:
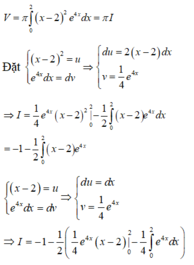
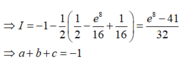
Đáp án C
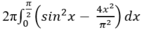


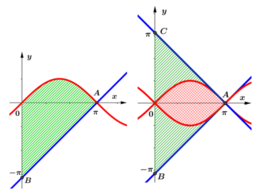
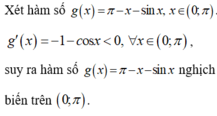
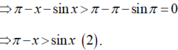

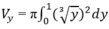
Chọn B.