Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

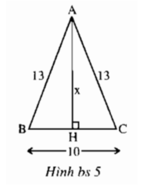
+) Xét ∆ AHB và ∆AHC có:
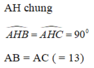
Suy ra: ∆ AHB = ∆AHC ( cạnh huyền – cạnh góc vuông).
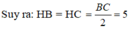
+) Tam giác AHB vuông tại H, áp dụng định lí Py- ta- go ta có:
AB2 = BH2 + AH2 suy ra: AH2 = AB2- BH2 = 132 – 52 = 144
Do đó, AH = 12.
Vậy x = 12.
Chọn đáp án D

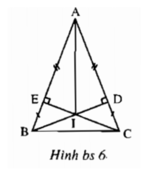
Chọn D. Năm cặp tam giác bằng nhau là:
ΔAEI = ΔADI, ΔBEI = ΔCDI, ΔAIB = ΔAIC, ΔBEC = ΔCDE, ΔABD = ΔACE.

Bài này có nhiều cách giải, ta có thể làm theo cách sau đây.
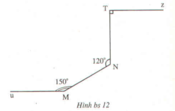
Từ điểm M vẽ đường thẳng Mn song song với đường thẳng TN.
+) Khi đó, vì ∠TNM + ∠NMn = 180° (hai góc trong cùng phía)
Mà ∠TNM = 120° nên ∠NMn = 60°.
+) Vẽ Mu’ là tia đối của Mu, biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Vì ∠uMN + ∠NMu’ = 180° (hai góc kề bù) biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Từ đó ∠nMu' = ∠NMn + ∠NMu' = 60° + 30° = 90°, tức là đường thẳng Mn vuông góc với đường thẳng Mu.
Do đường thẳng Mn song song với đường thẳng TN nên suy ra đường thẳng TN cũng vuông góc với đường thẳng Mu.
Từ đó Tz song song với Mu vì cùng vuông góc với TN.

Ta có: ∠C = 180o - 40o - 25o = 115o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn B

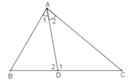
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
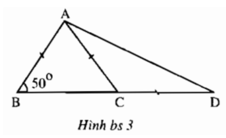
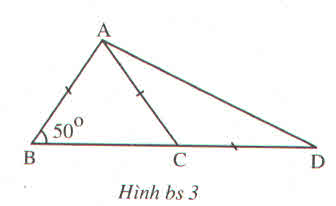
+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A
+) Tam giác ACD có góc ACB là góc ngoài của tam giác nên:
+) Lại có: AC = CD ( giả thiết) nên tam giác ACD cân tại C.
Chọn đáp án B