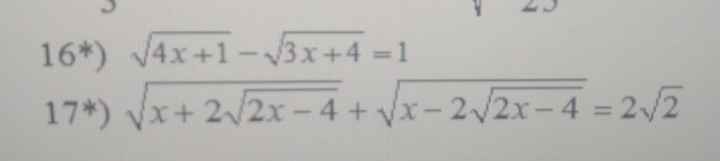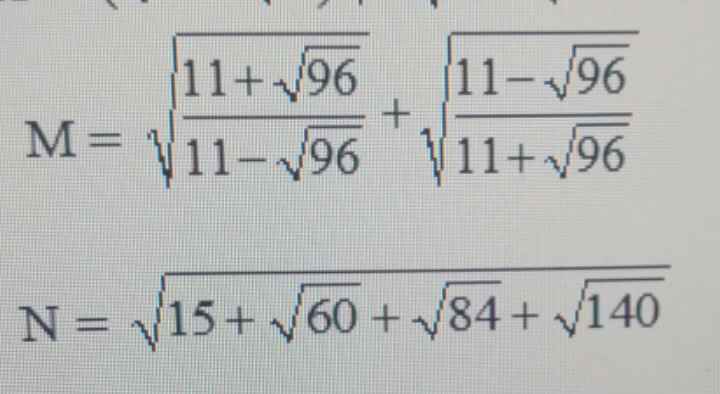K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 10 2021
a: Để (d)//y=x-3 thì \(4-m^2=1\)
\(\Leftrightarrow m\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
26 tháng 10 2021
16) ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
\(\sqrt{4x+1}-\sqrt{3x+4}=1\\ \Leftrightarrow\sqrt{4x+1}=1+\sqrt{3x+4}\\ \Rightarrow4x+1=1+3x+4+2\sqrt{3x+4}\\ \Leftrightarrow x-4=2\sqrt{3x+4}\\ \Leftrightarrow x^2-8x+16=12x+16\\ \Leftrightarrow x^2-20x=0\\ \Leftrightarrow x\left(x-20\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=20\end{matrix}\right.\)
Thử lại \(x=0\) không thỏa mãn \(\Rightarrow x=20\)
26 tháng 10 2021
\(M=\sqrt{\dfrac{11+\sqrt{96}}{11-\sqrt{96}}}+\sqrt{\dfrac{11-\sqrt{96}}{11+\sqrt{96}}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{121-96}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{121-96}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{25}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{25}}\)
\(\Rightarrow M=\dfrac{11+\sqrt{96}}{5}+\dfrac{11-\sqrt{96}}{5}\)
\(\Rightarrow M=\dfrac{22}{5}\)
26 tháng 10 2021
\(N=\sqrt{15+2\sqrt{15}+2\sqrt{21}+2\sqrt{35}}\\ N=\sqrt{3+5+7+2\sqrt{3}\sqrt{5}+2\sqrt{3}\sqrt{7}+2\sqrt{5}\sqrt{7}}\\ N=\sqrt{\left(\sqrt{3}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{3}+\sqrt{5}+\sqrt{7}\)
26 tháng 10 2021
\(P=A\left(3-x+2\sqrt{x}\right)=A\left(3-\sqrt{x}\right)\left(\sqrt{x}+1\right)\\ P=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\left(3-\sqrt{x}\right)\left(\sqrt{x}+1\right)=\left(2\sqrt{x}-1\right)\left(3-\sqrt{x}\right)\\ P=6\sqrt{x}-2x-3+\sqrt{x}=-2x+7\sqrt{x}-3\\ P=-2\left(x-2\cdot\dfrac{7}{4}\sqrt{x}+\dfrac{49}{16}-\dfrac{49}{16}\right)-3\\ P=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{49}{8}-3\le\dfrac{49}{8}-3=\dfrac{25}{8}\\ P_{max}=\dfrac{25}{8}\Leftrightarrow\sqrt{x}=\dfrac{7}{4}\Leftrightarrow x=\dfrac{49}{16}\)
15 tháng 4 2021
| x1 - x2 | ≥ 2
=> ( x1 - x2 )2 ≥ 4
<=> x12 - 2x1x2 + x22 ≥ 4
<=> ( x1 + x2 )2 - 4x1x2 ≥ 4
<=> m2 + 2m + 1 - 4m ≥ 4
<=> m2 - 2m - 3 ≥ 0
<=> ( m + 1 )( m - 3 ) ≥ 0
đến đây dễ rồi
13 tháng 2 2017
Hãy nhớ là đừng đăng câu hỏi linh tinh trên diễn đàn kẻo bị trừ điểm!