
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 8:
\(x^2+\left(2m+1\right)x-m^2=0\)
a=1; b=2m+1; c=-m2
Vì ac<=0 nên phương trình luôn có nghiệm
Theo đề, ta có: \(A=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(2m+1\right)^2-8\left(-m^2\right)\)
\(=4m^2+4m+1+8m^2=12m^2+4m+1\)
\(=12\left(m^2+\dfrac{1}{3}m+\dfrac{1}{12}\right)\)
\(=12\left(m^2+2\cdot m\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{18}\right)\)
\(=12\left(m+\dfrac{1}{6}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\forall m\)
Dấu '=' xảy ra khi m=-1/6

\(=\dfrac{\sqrt{x}+2-\sqrt{x}}{x-4}\cdot\dfrac{x+2}{1}=\dfrac{2\left(x+2\right)}{x-4}=\dfrac{2x+4}{x-4}\)


\(\left\{{}\begin{matrix}x=5-y\\y\left(5-y\right)=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\end{matrix}\right.\)

a) Thay m = -2 vào (P) ta có:
\(y=\left(-2-3\right)x+\left(-2\right).\\ \Leftrightarrow y=-5x-2.\)
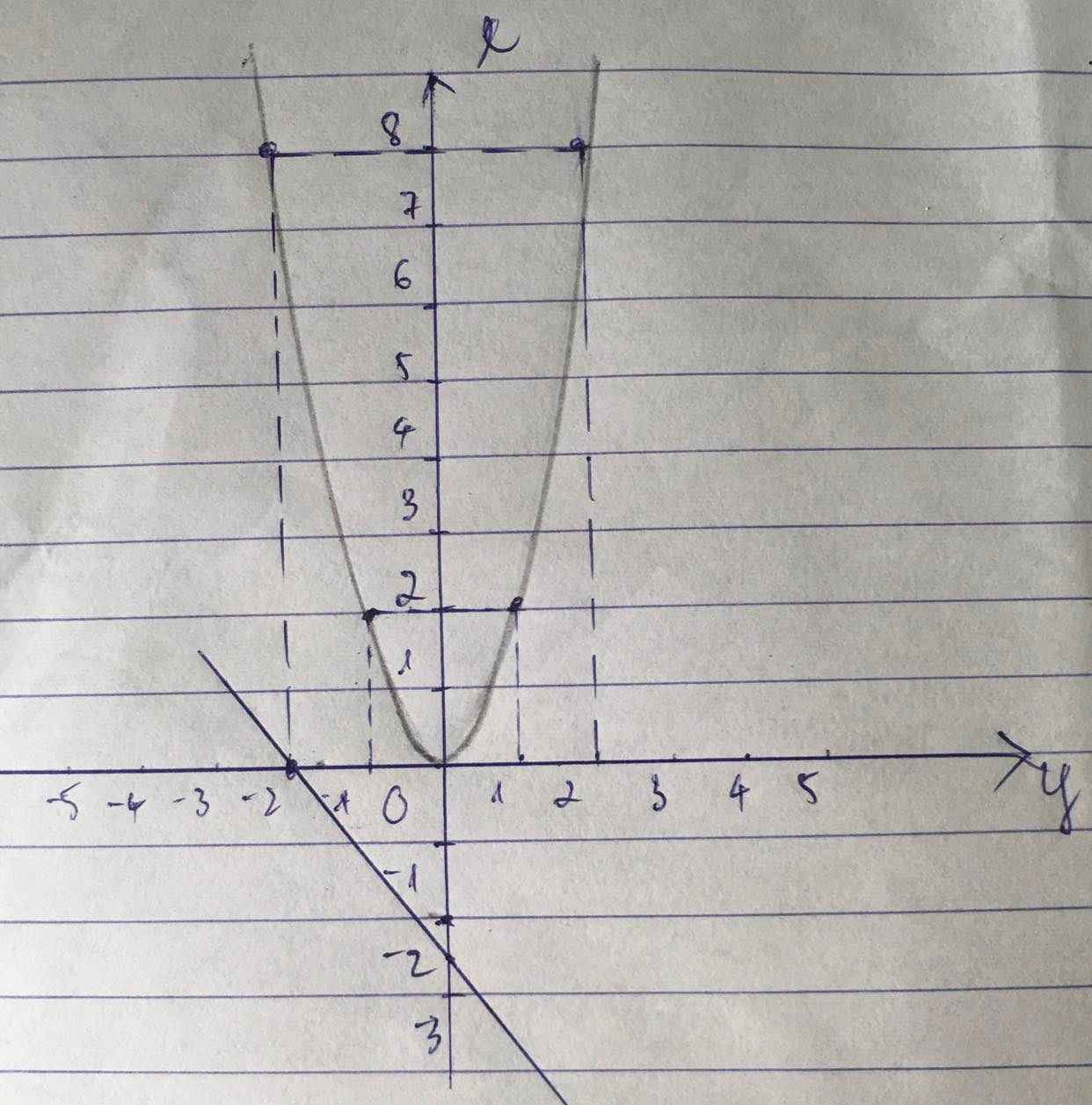
i) + \(y=-5x-2.\)
\(Cho\) \(x=0.\Rightarrow y=-2.\)
\(Cho\) \(y=0.\Rightarrow x=\dfrac{-2}{5}.\)
+ \(y=2x^2.\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |


a: Xét tứ giác MAOB có \(\widehat{OAM}+\widehat{OBM}=180^0\)
nên MAOB là tứ giác nội tiếp
Xét ΔMBD và ΔMCB có
\(\widehat{MBD}=\widehat{MCB}\)
\(\widehat{BMD}\) chung
Do đó: ΔMBD\(\sim\)ΔMCB
Suy ra: MB/MC=MD/MB
hay \(MB^2=MC\cdot MD\left(1\right)\)
b: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên OM là đường trung trực của AB
Xét ΔOBM vuông tại B có BH là đườg cao
nên \(MH\cdot MO=MB^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MC=MH\cdot MO\)

ĐKXĐ: x>=-3/2
\(2x-3\sqrt{2x+3}-7=0\)
=>\(2x+3-3\sqrt{2x+3}-10=0\)
=>\(2x+3-5\sqrt{2x+3}+2\sqrt{2x+3}-10=0\)
=>\(\sqrt{2x+3}\left(\sqrt{2x+3}-5\right)+2\left(\sqrt{2x+3}-5\right)=0\)
=>\(\left(\sqrt{2x+3}-5\right)\left(\sqrt{2x+3}+2\right)=0\)
=>\(\sqrt{2x+3}-5=0\)
=>\(\sqrt{2x+3}=5\)
=>2x+3=25
=>2x=22
=>\(x=\dfrac{22}{2}=11\)

Bài 5:
a: Để đây là hàm số bậc nhất thì m+5<>0
hay m<>-5


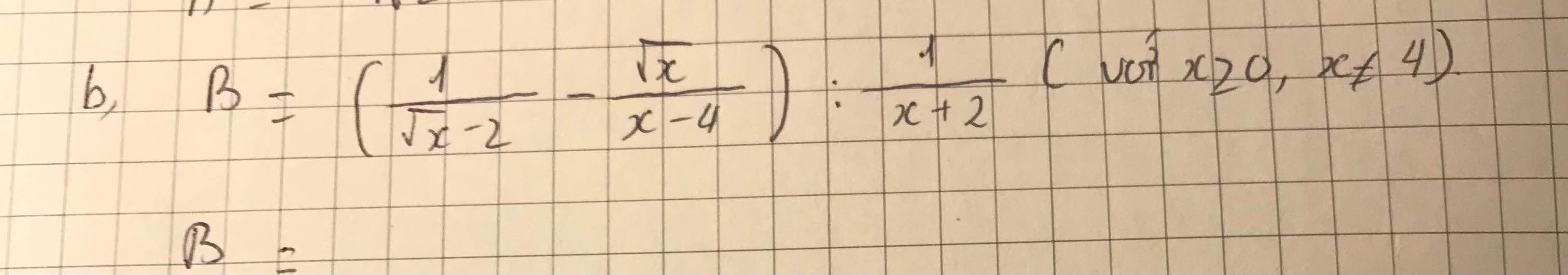






6:
a: Xét ΔABH vuông tại H có \(cosB=\dfrac{BH}{AB}\)
=>\(cosB=\dfrac{4}{16}=\dfrac{1}{4}\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{16}{BC}=\dfrac{1}{4}\)
=>BC=64(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=64^2-16^2=3840\)
=>\(AC=\sqrt{3840}=16\sqrt{15}\left(cm\right)\)
b: Xét ΔABN vuông tại A có AD là đường cao
nên \(BN\cdot BD=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BN\cdot BD=BH\cdot BC\)