
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
b: Xét ΔOAC và ΔOBD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔOAC=ΔOBD
Nếu cậu làm hết thì tớ sẽ thả đúng và một lượt theo dõi:3(không làm cũng không sao tớ cảm ơn)



A= 3/4 +2/5-7/5+5/4
= (3/4 + 5/4) + (2/5-7/5)
= 2 + (-1)
= 1

Ta có :
\(x^2=\frac{24}{25}\)
\(\Rightarrow x=\pm\sqrt{\frac{24}{25}}\)
\(\Rightarrow x\in\left\{\sqrt{\frac{-24}{25}};\sqrt{\frac{24}{25}}\right\}\)

Tham khảo:
a) Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
MI=NI(gt)
Do đó: ΔIMC=ΔINC(hai cạnh góc vuông)
b) Ta có: ΔIMC=ΔINC(cmt)
nên ˆMCI=ˆNCIMCI^=NCI^(hai góc tương ứng)
hay ˆBCA=ˆKCABCA^=KCA^
Xét ΔBAC vuông tại A và ΔKAC vuông tại A có
AC chung
ˆBCA=ˆKCABCA^=KCA^(cmt)
Do đó: ΔBAC=ΔKAC(cạnh góc vuông-góc nhọn kề)
⇒CB=CK(hai cạnh tương ứng)
Ta có: MI⊥AC(gt)
AB⊥AC(ΔABC vuông tại A)
Do đó: MI//AB(Định lí 1 từ vuông góc tới song song)
hay MN//KB
Xét ΔCKB có
M là trung điểm của CB(gt)
MN//KB(cmt)
Do đó: N là trung điểm của CK(Định lí 1 đường trung bình của tam giác)
c) Ta có: MA=ME(gt)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(cmt)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
hay AB//EC(Hai cạnh đối trong hình bình hành ABEC)
d) Ta có: ABEC là hình bình hành(cmt)
nên AB=EC(Hai cạnh đối trong hình bình hành ABEC)
mà AB=AK(ΔCBA=ΔCKA)
nên EC=AK
Ta có: AB//EC(Cmt)
nên CE//KA
Xét tứ giác AECK có
CE//AK(cmt)
CE=AK(cmt)
Do đó: AECK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Xét ΔCAB có
M là trung điểm của BC(gt)
MI//AB(cmt)
Do đó: I là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: AECK là hình bình hành(cmt)
nên Hai đường chéo AC và EK cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của AC(cmt)
nên I là trung điểm của EK
hay E,I,K thẳng hàng(đpcm)

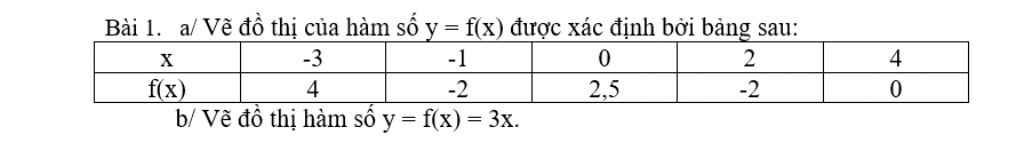
 giúp tớ bài này với ạ:3 tớ đang cần gấp
giúp tớ bài này với ạ:3 tớ đang cần gấp


