K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 10 2021
a) \(x=x_0+v_0t+\dfrac{1}{2}at^2=10+5t+\dfrac{1}{2}\cdot1\cdot t^2=10+5t+0,5t^2\)
b) Sau 20s:
Vận tốc vật: \(v=v_0+at=5+1\cdot20=25\)m/s
Vật cách gốc tọa độ: \(x=10+5\cdot20+0,5\cdot20^2=310\left(m\right)\)
6 tháng 11 2016
vận dụng công thức sau để giải:
∆x = (v0+v).∆t / 2
∆t là thời gian vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.
Lưu ý ở bài này giây thứ 1 tính từ thời điểm t=0 đến t=1
Giây thứ 4 tính từ thời điểm t=3 đến t=4
(**) Công thức không phụ thuộc thời gian trong chuyển động thẳng biến đổi đều :
v^2 - v0^2 = 2.a.∆x
Với a là gia tốc, vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.
NT
3
4 tháng 12 2021
Độ dãn của lò xo:
\(F_{đh}=k\cdot\Delta l\Rightarrow\Delta l=\dfrac{F_{đh}}{k}=\dfrac{2}{100}=0,02\)m=2cm
DT
10 tháng 3 2022
Áp dụng định luật Bôi – Lơ – Mariot cho quá trình đẳng nhiệt ( nhiệt độ không đổi) ta có:
\(pv=const\Leftrightarrow p_1v_1=p_2v_2=2.10^5.10=1,25.10^5.v_2\)
\(\Rightarrow v_2=\dfrac{2.10^5.10}{1,25.10^5}=16\left(lít\right)\)
25 tháng 9 2021
a) Vận tốc khi vật chạm đất:
Ta có:\(v^2-v^2_0=2as\Leftrightarrow v=\sqrt{2as+v^2_0}=\sqrt{2.10.500+0^2}=100\left(m/s\right)\)
b) Vận tốc đạt đc sau 1s:
Ta có: \(v_1=v_0+at=0+10.1=10\left(m/s\right)\)
c) Thời gian từ lúc thả đến lúc chạm đất:
Ta có: \(v=v_0+at\Leftrightarrow t=\dfrac{v-v_0}{a}=\dfrac{100-0}{10}=10\left(s\right)\)
d) Quãng đường vật đi đc sau 0,5s:
\(s=v_0t+\dfrac{1}{2}at^2=0.0,5+\dfrac{1}{2}.10.0,5^2=1,25\left(m\right)\)
e) Quãng đường từ lúc thả cho đến khi đạt vận tốc 4m/s:
Ta có: \(v^2-v^2_0=2as\Leftrightarrow s=\dfrac{v_2^2-v_0^2}{2a}=\dfrac{4^2-0^2}{2.10}=0,8\left(m\right)\)
Giải
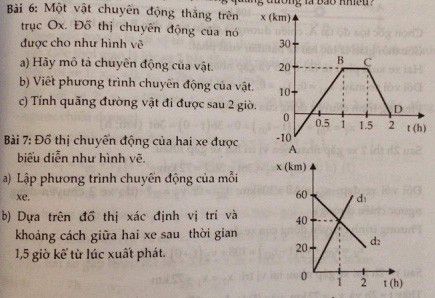
a. Phương trình chuyển động của hai xe
Xe ô tô: x1=30t
Xe mô tô: x2= 100 - 20t
b. Đồ thị toạ độ- thời gian, xác định
vị trí và thời điểm hai xe gặp nhau.
+ Chọn hệ toạ độ như hình vẽ:
+ Đồ thị toạ độ:
Của ô tô: Đoạn thẳng OM
Của mô tô: Đoạn thẳng PM
+ Vị trí hai xe gặp nhau: Cách gốc tạo độ 60km, thời
điểm hai xe gặp nhau là lúc 2h